:) Sayrus: Znajdz wszystkie parametry m,dla ktorych uklad rownan ma 4 rozwiazania.

⎧	|x|+|y|=2
⎩	x2+y2=m2

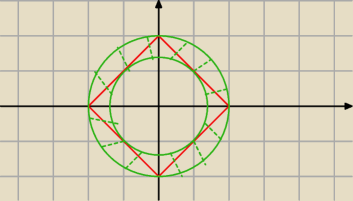
razor: na czerwono wykres |x|+|y| = 2 x²+y² = m² to równanie okręgu o środku w punkcie (0,0) i promieniu równym m, który będzie przecinał czerwony wykres kiedy okrąg będzie w pozycjach "pomiędzy" okręgiem wpisanym i opisanym razem z tymi okręgami (nie umiem tego za dobrze opisać, mam nadzieję że wiadomo o co chodzi Długość boku tego kwadratu to √2²+2² = 2√2, zatem promień okręgu wpisanego = √2, promień okręgu opisanego = 2 m ∊ <√2, 2> m ≥ √2 i m ≤ 2 m² ≥ 2 i m² ≤ 4 m ∊ <−2, −√2> ∪ <√2, 2> niech ktoś sprawdzi jeszcze

pigor: ... równanie |x|+|y|=2 ⇔ y= −|x|+2 v y=|x|−2 − kwadrat o wierzchołkach (−2,0),(0,2),(2,0)(0,−2) w układzie xOy, zatem układ równania okręgu x²+y²=m² z powyższym równaniem ma 4 rozwiązania ⇔ m²=2 ⇔ |m|=√2 ⇔ m∊{−√2,√2} . ...

pigor: tak razor masz rację; ja uwzględniłem tylko ... niestety .

razor: ja też się pomyliłem, będzie tylko okrąg wpisany i opisany, bo przecież w innych przypadkach będzie 8 rozwiązań zatem już finalna odpowiedź (chyba ) to m ∊ {−2,−√2,√2,2}

pigor: ... ale chyba te przedziały są m∊ [−√2;−1] U [1;√2] . ... lub coś koło tego

pigor: ... no tak ; jasne ja też ..., ale tak rysunek ma i niech sobie zainteresowany odczyta co ... trzeba , ja się wyłączam ...

Sayrus: dzieki chlopaki