trojkaty Algebra: Oblicz długość przeciwprostokątnej trójkąta prostokątnego, którego obwód jest równy 70 cm, a pole wynosi 210 cm². Rozwiązanie: ( skad to jest (a + b)² − 2ab = c² ) c = ? Ob = 70cm P = 210cm² Ob = a + b + c P = 1/2 * a * b a + b + c = 70 1/2 * a * b = 210 a² + b² = c² a + b + c = 70 ⇒ a + b = 70 − c a * b = 420 (a + b)² − 2ab = c² (a + b)² − 2ab = c² (70 − c)² − 2 * 420 = c² 4900 − 140c + c² − 840 = c² −140c = 840 − 4 900 −140c = −4060 c = 29cm −−−−−−−−− odpowiedź

miecio: rozpisz to będziesz wiedzieć (podnieś do kwadratu)

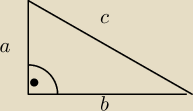
Algebra: ale twierdzenie cosinosow w tej sytuacji to c²=a²+b²−2*a*b*cos 90stopni

Algebra: a nie (a + b)² − 2ab = c²

Algebra: z czego to wynika

ZKS: (a + b)² − 2ab = a² + 2ab + b² − 2ab = a² + b²

Algebra: DZIEKI WIELKIE − TERAZ KJUMAM