Przekształcenia wykresów funkcji Pat: Punkty A(−4, 2), B(−2, −6), C(4, 4) są wierzchołkami trójkąta. a) Oblicz odległość środka ciężkości S trójkąta od wierzchołka A. b) Wyznacz współrzędne punktu D tak, aby czworokąt ABCD był równoległobokiem. Bardzo proszę o rozwiązanie zadania. Pozdrawiam

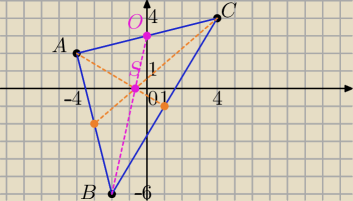
Mila: Punkty A(−4, 2), B(−2, −6), C(4, 4) S− Srodek ciężkości ΔABC− punkt przecięcia środkowych. wsp.

	−4+(−2)+4		2+(−6)+4
S=(xs,ys)=		,		)
	3		3

	−2
S=(		,0)
	3

|SA|=√(−4+(2/3))²+(2−0)²= oblicz b) O− środek AC

	−4+4		2+4
O=(		,		)=(0,3)
	2		2

Punkt O jest środkiem przekątnej BD

	xd+(−2)		yd+(−6)
(0,3)=(		,		)
	2		2

Dokończ