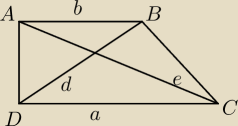
pomocy aaaaaa: Oblicz długości podstaw trapezu prostokątnego (a >b) wiedząc, że długości przekątnych to e = 10 i f = 6√2

Hugo: z pitagorasa ?

zawodus: A mnie się wydaje, że za mało danych

Hugo: zawodus, to nie twój poziom

Eta: Nie da się

zawodus: Rzeczywiście nie mój poziom nawet ja nie potrafię rozwiązać zadań, które mają niekompletną treść

aaaaaa: ja wyliczyłam tylko że a² − b² = 28, ale nie wiem co moge dalej z tym zrobić

Hugo: Eto wiary ! Razem − kiedy już zbudujemy nasz wspólny kościół EhuTsiaA ten dzień przejdzie do historii !

sushi_ gg6397228: (a+b)(a−b)= 1*28 (a+b)(a−b)= 2*14 (a+b)(a−b)= 4*7 podstawiaj i kombinuj, która para pasuje

Hugo: Uważam że zadanie da sie rozwiązać bo jest wstawka prostokątny i nie da sie go byle jak rozwiazac

Hugo: sushi widzę od nie dawna pacyfikuje nieuków

Zeus: od niedawna, a nie od nie dawna

aaaaaa: a gdyby oznaczyć a jako b+ x, wtedy x = a − b, i to jakoś wykorzystać

aaaaaa: .

Toskan: Rysunek przedstawia dwa trapezy: http://avatars.zapodaj.net/images/58b82f2bbac4.png Pierwszy z nich o współrzędnych A(−5, 0); B(3, 0); C(1, 6); D(−5, 6) oraz długości boków a=8, b=6 wysokości h=6 Drugi z nich A(−5, −1−√37); B(−5+3√7, −1−√37), C(−5+√35, −1), D(−5, −1) oraz długości boków a=3√7; b=√35 wysokości h=√37 Oba są prostokątne i z Pitagorasa łatwo wyznaczyć długości przekątnych. Teraz zadanie. Przez h oznaczmy wysokość. Z Pitagorasa mamy: h² = 72 − b² = 100 − a² b² = a² − 28 Wobec założeń a>0; b>0; a>b b = √a² − 28, gdy a² − 28>0, czyli a>2√7