Ciągi
kama: Oblicz dla jakich n(chyba, bo już nie pamiętam dobrze) ciąg an=−n2+11x+7 przyjmuje wartości
nie większe od 2
9 cze 22:27
Eta:
an≤2
teraz rozwiąż nierówność
−n2+11n+7≤2 i n∊N+
9 cze 22:29
kama: −2n
2+11n+5≤0 Tam pomyliłam się
Δ=121−4*5*(−2)
Δ=161
√Δ=
√161
| | −11−√161 | | −11+√161 | |
n1= |
| n2= |
| |
| | −4 | | −4 | |
n
1≈5,9 n
2≈−0,4 ( na osi zaznaczyłam normalnie ale później do rozwiązania będzie
wygodniej.
Wyszło mi n∊<+,+
∞)
9 cze 22:40
zawodus: Skąd taka odpowiedź?
9 cze 22:41
sushi_ gg6397228:
dzisiaj jest "kumulacja " w LOTTO, więc wszyscy strzelają z liczbami
9 cze 22:45
kama:
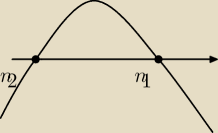
A skoro n∊N
+ no to dalej poszło. Chyba, że coś pomyliłam, a jak powinno wyjść?
9 cze 22:46
kama: Tam odpowiedź miała być <6,+∞), coś nie wskoczyło.
9 cze 22:47
Eta:
Raz piszesz −n2+11n+7≤2 a drugi raz : −2n2+11n+7≤2
to w końcu jak ma być?
9 cze 22:48
sushi_ gg6397228:
to liczymy na piechotę
a1=...
a2=...
a3=....
myślimy i dajemy odp
9 cze 22:48
kama: To 2. napisałam, że tam popełniłam błąd. Przepraszam jeśli sprawiło to tyle kłopotów.
9 cze 22:48
sushi_ gg6397228:
przecież "n" jest naturalne, więc zapis <6; +∞) jest do bani
9 cze 22:57
kama: <6,+∞), to jest źle? napisze chociaż ktoś odpowiedź a resztę sama pomyśle
9 cze 22:57
kama: A no tak przepraszam, taki błąd {6,7,8...}
9 cze 22:58
sushi_ gg6397228:
bo w tym zbiorze sa np √1234567; 100+√2, a czy istnieją wyrazy o takim indeksie ?
9 cze 22:58
sushi_ gg6397228:
a5=....
9 cze 22:59
kama: a5=10
9 cze 23:03
Hugo: no kaman
9 cze 23:04
sushi_ gg6397228:
to było sprawdzenie czy dobrze sie policzyło
odp o 22.58 jest w miare zadawalająca
9 cze 23:05
kama: Ej a patrzcie na dobrą nierówność, bo później się poprawiłam i tam jest − 2n2+11n+5<równe 0
9 cze 23:07