Trójkąt wpisany w okrąg AAA: Cześć, proszę o pomoc przy tym zadaniu: W okrąg o(O,3√2) wpisano ostrokątny trójkąt równoramienny ABC, którego długość podstawy AB jest równa 6. Oblicz o ile pole trójkąta ABC jest większe od pola trójkąta ABO.

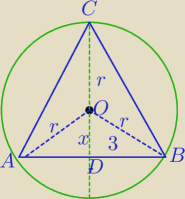
Mila: r=3√2 2r=6√2>6 AB leży poniżej środka okręgu , patrząc od góry, od punktu C (Δostrokątny) Wystarczy ta wskazówka ?

AAA: Nie wystarczy

Mila: Czego nie rozumiesz?

Mihau: Aj, przepraszam nie to zadanie podałem To zrobiłem chodziło mi o to: W okrąg o (O,r) wpisano trójkąt równoramienny ABC, którego ramiona mają długość 6 i tworzą kąt o mierze 60. Oblicz o ile pole trójkąta ABC jest większa od pola trójkąta ABO.

Mila: Rysunek może być ten sam. Skoro kąt między ramionami ma 60^o⇔ΔABC jest Δrównobocznym o boku dł. 6.

	62√3
PΔABC=		=9√3
	4

	6√3
h=		=3√3
	2

R=2√3 x²+3²=(2√3)² x²=12−9 x=√3

	1
PΔABO=		*6*√3=3√3
	2

dokończ.