Ekstrema funckji Radek: Ekstrema funkcji Mam taki przykład funkcji:

3x−2
x+3

Obliczyłem pochodną

11
(x+3)2

I mam wyznaczyć ekstremum więc przyrównuje do 0

11
	=0 i jak to obliczyć ?
(x+3)2

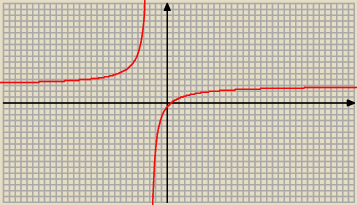
Janek191: Ta pochodna jest > 0 dla x ≠ − 3 , a to oznacza, ze funkcja rośnie w całej swej dziedzinie

Janek191: D = R \ { − 3}

Radek: Więc jak mam zapisać jak jestem na etapie

11
	=0 ?
(x+3)2

Janek191:

	11
Trzeba zapisać		≠ 0 dla x ∊ R \ { − 3} − brak ekstremum
	( x + 3)2

Radek: To wtedy tabelki się nie rysuje ?

Janek191:

	11
Trzeba zapisać		≠ 0 dla x ∊ R \ { − 3} − brak ekstremum
	( x + 3)2

Radek: To wtedy tabelki się nie rysuje ?

PW: Janek191, co Ty napisałeś pod rysunkiem o 18:59.

daras: tabelki są tylko pomocnicze i nigdy nie trzeba ich rysować wystarczy, że się namaluje kształt tej funkcji a funkcja jest rosnąca więc nie ma NIGDZIE maksimum

daras: trzeba za to pobadać jak się zachowuje na końcach przedziału określoności lim x−>±∞ i lim x−>−3 z lewej i z prawej => 2 asymptoty

PW: Janek191 już tu nie zagląda, więc wyjaśnię o czym pisałem 9 czerwca o 21:04. To nieprawda, że badana funkcja jest rosnąca w całej dziedzinie. Nie ma takiego twierdzenia, które pozwala wnioskować, że skoro f'(x) > 0 dla x∊D, to f jest rosnąca na D (nie ma, bo jest fałszywe − wystarczy popatrzeć na rysunek z 18:59; funkcja ta jest rosnąca na przedziale (−∞,−3) i jest rosnąca na przedziale (−3,∞), ale nie jest rosnąca na całej dziedzinie).

J: PW , a co jest dziedziną tej funkcji ?

wredulus_pospolitus: J ... D_f = R\{−3} f(x) rosnąca w (−∞,−3), w (−3,∞) ≠ rosnąca w całej dziedzinie (pomimo tego, że suma tych dwóch przedziałów jest równa dziedzinie) Powód jest bardzo prosty −−− funkcja rosnąca w danym przedziale spełnia warunek: ∀_x1,x2∊A x₁<x₂ => f(x₁)<f(x₂) a przecież to nie jest spełnione dla CAŁEJ dziedziny

zawodus: Nie dokładnie rozumiem pytanie, ale dziedziną badanej funkcji jest oczywiście R\{−3}

zawodus: Dlatego zawsze powtarzam, żeby pisać przedziały po przecinku, bo jak nie to

J: Przekonałeś mnie "wredulus" ... Wycofuję pytanie ...

daras: ja bym ujął to tak: "na pewno nie jest malejąca"