Ostrosłupy-prosze o pomoc Radek: Dany jest ostrosłup trójkątny, którego podstawą jest trójkąt równoramienny o bokach długości 5 cm, 5 cm i 6 cm. Wysokość ostrosłupa jest równa 2 cm. Spodek wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz pole powierzchni całkowitej tego ostrosłupa.

AROB: pomagam

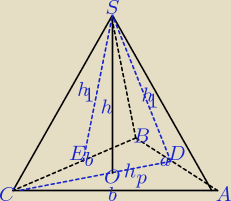
AROB: Najpierw poślę rysunek bryły, a oddzielnie rysunek podstawy z rozwiązaniem ( bo trudno zmieścić).

AROB:

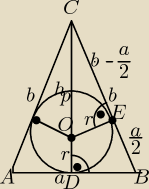
AROB: Dane: a=6cm, b= 5cm, h= 2cm, obl. P_c

	1		1		1
Pc =		ahp +		ah1 + 2 *		bh1
	2		2		2

Z ΔBCD obliczam wysokość podstawy h_p :

	a
hp2 + (		)2 = b2
	2

h_p² + 9 = 25 ⇒ h_p² = 16 ⇒ h_p = 4 cm ΔBCD ∼ ΔCOE

	a   b −   2		hp
Stąd:		=
	r		a   2

5 − 3		4		3
	=		⇒ r =
r		3		2

Wysokości ścian bocznych są równej długości. Obliczam h_b z ΔODS : h² + r² = h₁²

	3
h12 = 22 + (		)2
	2

	9
h12 = 4 +
	4

	1		25		5
h12 = 6		=		⇒ h1 =
	4		4		2

	1		1		5		5
Pc =		* 6 * 4 +		*6*		+ 5 *		=
	2		2		2		2

	15		25
= 12 +		+		= 12 + 20 = 32 [cm2]
	2		2

mila0510: ∞w trójkącie równoramiennym ramię ma długość 8 i tworzy z podstawą kąt 30 stopni. oblicz pole trójkąta oraz dłudość promienia okręgu opisanego na tym trójkącie. proszę o pomoc!

AROB: pomagam

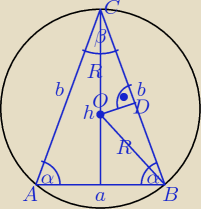
AROB: Dane: b = 8, α = 30⁰, P_ABC, R = ? β = 180⁰ − 2*30⁰ = 120⁰

	1		1		1
PABC =		b2 * sinβ =		* 82 * sin1200 =		* 64 * sin(900 + 300) =
	2		2		2

	√3
= 32*cos300 = 32 *		= 16√3 [j2]
	2

Trójkąt OBC jest równoramienny. Środek okręgu opisanego na trójkącie leży w punkcie przecięcia się symetralnych jego boków, zatem symetralna h dzieli kąt β na połowy. Stąd z ΔCOD obliczam promień okręgu opisanego R:

	b   2		β
		= cos
	R		2

4
	= cos600
R

4		1
	=		⇒ R = 8
R		2

karlos:

	abc
A nie prościej r wyznaczyć z wzoru PABC=p*r (p=		czyli połowa obwodu).
	2

Czyli 12=rp p=8

	12
r=
	4

	3
r=
	2