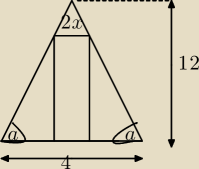
 Przedstaw pole P prostokąta jako funkcję zmiennej x. Dla jakiego argumentu x pole jest
największe? Podaj wymiary prostokąta o największym polu.
(rysunek: kąty oczywiście α, nie a. Na górze 2x, z prawej 12, na dole 4)
Przedstaw pole P prostokąta jako funkcję zmiennej x. Dla jakiego argumentu x pole jest
największe? Podaj wymiary prostokąta o największym polu.
(rysunek: kąty oczywiście α, nie a. Na górze 2x, z prawej 12, na dole 4)
| 12 | ||
tg α = | = 6 | |
| 2 |
| h | h | |||
tg α = | = | ⇒ h = ( 2 − x)*tg α = ( 2 − x)*6 = 12 − 6x | ||
| y | 2 − x |
| − 24 | ||
Funkcja kwadratowa P przyjmuje największą wartość dla x = | = 1 | |
| −24 |
 !
!