Wyznacz t, wiedząc, że punkty: A, B, C należą do tej samej prostej.
marlc:
Wyznacz t, wiedząc, że punkty: A, B, C należą do tej samej prostej.
a) A(t,0), B(−2, −6), =(2, −3)
b) A(−4, −5), B(5,t), C(2, 1)
9 cze 08:39
zawodus: w czym tkwi problem?
9 cze 08:42
9 cze 08:43
marlc: Chodzi o to żeby jak najbardziej rozpisać to

9 cze 08:46
zawodus: Jeden ze sposobów (nie najszybszy)
1. równanie prostej BC
2. prosta AB, to prosta równoległa. (wyznaczasz t).
9 cze 08:50
marlc: Nie ogrniam matmy −.−
9 cze 08:57
zawodus: gotowiec nic ci nie da...
9 cze 09:14
marlc: Niestety wiem ... Muszę zacząć chodzić na korepetycje bo porażka a teraz jakoś muszę to zdać
−.−
9 cze 09:22
PW: a) Szybko można zrobić tak:
wektor BC wyznacza prostą w tym sensie, że dla dowolnego punktu X na tej prostej
(1) BX→ = k•BC dla pewnej k∊R
i odwrotnie − jeżeli istnieje k∊R, taka że BX→ = k•BC, to X należy do prostej wyznaczonej
przez punkty B i C.
U nas [BC→] = [2−(−2), −3−(−6)] = [4, 3], X = A = (t, 0), a więc [BX→] = [t−(−2), 0−(−6)] =
[t+2, 6].
Musi być więc − po podstawieniu do (1) −
[t+2, 6] = k•[4,3] dla pewnej k∊R.
t+2 = 4k i 6 = 3k,
skąd k=2 i t = 6.
Dla sprawdzenia możesz policzyć, że wtedy |AB| = 10, |AC| = 5, |BC| = 5, a więc
|AB| = |AC| + |CB|
− spełniony jest warunek współliniowości punktów i przy okazji widać, że C leży między A i B.
9 cze 12:17
the end:
porażka wszystkich oprócz osoby o nicku wielokropek
9 cze 12:41
PW: Cytat:
Chodzi o to żeby jak najbardziej rozpisać to.
Sądzisz, że osoba o nicku wielokropek spełniła oczekiwania marlc?
the end − ten nick oznacza, że to ostatni taki komentarz?
9 cze 13:59
54: hejka
12 kwi 21:44
Pr713: 1. równanie prostej BC
2. prosta AB, to prosta równoległa. (wyznaczasz t)

2. Do równania prostej BC, wstawiasz współrzędne punktu A(t, 0) − wyznaczasz t
np. y = 2x+1 ⇒ 0 = 2t+1 ⇒ t=−
12
12 kwi 22:39
Eta:
| | 3 | | −3−0 | | 3 | |
to aAC= |
| = |
| = |
| ⇒ t−2=4 ⇒ t=6 |
| | 4 | | 2−t | | t−2 | |
2) analogicznie
| | 1−t | |
to aBC=1= |
| ⇒ 1−t= −3 ⇒ t=4 |
| | 2−5 | |
12 kwi 22:58
Eta:
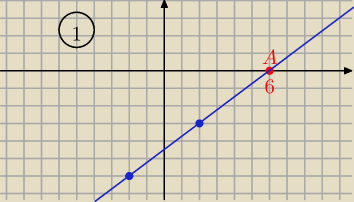
12 kwi 23:06
Eta:
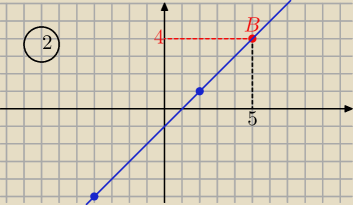
12 kwi 23:10
PATMAT16: Można też tak.
A(t;0)
B(−2;−6)
C(2;−3)
BC:
−6−3=2b
−9=2b /:2
Podstawiamy "b" pod dowolne równanie z układu równań:
−6=4a−9
3=4a /:4
Zapiszmy sobie równanie prostej BC w postaci kierunkowej, a potem przekształćmy na ogólną:
3x−4y−18=0
Teraz możemy obliczyć współrzędną "t" z odległości punktu A od prostej BC, wiedząc, że jeżeli
punkt A należy do tej prostej to jego odległość od niej jest równa 0:
|3t−18|=0
3t−18=0 /:3
t−6=0
t=6
Analogicznie drugi przykład

12 kwi 23:35
Eta:
Za dużo obliczeń

Czas na maturze jest "droższy od pieniędzy"

12 kwi 23:40

 2. Do równania prostej BC, wstawiasz współrzędne punktu A(t, 0) − wyznaczasz t
np. y = 2x+1 ⇒ 0 = 2t+1 ⇒ t=−12
2. Do równania prostej BC, wstawiasz współrzędne punktu A(t, 0) − wyznaczasz t
np. y = 2x+1 ⇒ 0 = 2t+1 ⇒ t=−12



 Czas na maturze jest "droższy od pieniędzy"
Czas na maturze jest "droższy od pieniędzy" 