planimetria Pati :) : Szukam, szukam , szukam rozwiązań na necie, ale znaleźć nie mogę do niektórych, dlatego liczę, ze mi pomożecie Zostało mi kilka zadań do zrobienia... zad. 4 b) Dany jest trójkąt ABC o polu 54 cm². Oblicz pole trójkąta CDE takiego, że punkt D należy do boku AC, punkt E należy do boku AB i AD/DC=2/3. (rysunek mam, ale nie wiem, co dalej, wyniki mają być: 19,44; 8,64). zad. 22

	a2−b2
Mając odcinki o długościach a i b, skonstruuj odcinek o długości x=		. (nie mam
	a+2b

pojęcia jak sie za to zabrać) zad. 23 Mając odcinki o długościach a i b, skonstruuj odcinek o długości x takiej, że

	1		1		1		1
		=		(		+		).
	x		3		a		b

Jak ktoś wie, jak zrobić cokolwiek , to pomóżcie, bo pilnie mi potrzeba.

sushi_ gg6397228: to juz dzisiaj na forum Ktoś wrzuca takie zadania

Pati :) : zauważyłem, ale nikt ich nie rozwiązał

diana7: 23. Było dzisiaj coś podobnego na forum: Bierzemy sobie dowolny trapez ABCD, w którym podstawy AB, CD są równe odpowiednio b, a, S jest punktem przecięcia przekątnych. Niech K będzie punktem przecięcia prostej równoległej do AB,

	CS		a		ab
przechodzącej przez S z bokiem AD. Z tw. Talesa		=		, zatem KS=		.
	SA		b		a+b

	ab
Łatwo zatem skonstruować odcinek długości 3		, który jest równy
	a+b

	1
		.
	13(1a+1b)

diana7: 22. możesz poszukać w moich postach. 4. Pole tego trójkąta może być różne w zależności od położenia punktu E. Czy treść jest na pewno dobrze przepisana?

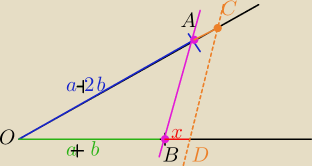
Mila: Zadanie 2)

	(a+b)*(a−b)
x=		i założenie : a>b
	a+2b)

⇔

x		a+b
	=		⇔
a−b		a+2b

a+2b		a−b
	=
a+b		x

Skorzystamy z tw. Talesa 1)Najpierw rysujesz dwa odcinki : a, b, a>b a) budujesz odcinek a+2b, a−b, a+b b) na ramionach kąta odkładasz jak na rysunku: a+2b, a+b i rysujesz prostą AB, potem odkładasz AC=a−b i rysujesz równoległą CD BD=x