geometria Luiza: W trójkącie ostrokątnym ABC, kąt ABC=60stopni. Odcinki AM I CN są wysokościami trójkąta ABC, Q jest środkiem boku AC. Znajdź miary kątów trójkąta NMQ. Proszę o pomoc w zadaniu.

PW: Ja też podejrzewam, że zawsze trójkąt NMQ będzie równoboczny, ale dowód nie jest taki prosty. Dlaczego założyłaś, że ABC jest równoboczny (ściślej: postawiłaś taką tezę i ją udowodniłaś, choć gdzieś musiałaś "oszukać") − generalnie ΔABC nie jest równoboczny, bo nie byłoby czego dowodzić. Można popatrzeć tak: mamy dany odcinek AB i półprostą nachyloną do niego pod kątem 60°. Na półprostej tej jest stały punkt M, taki że AM⊥MB. Punkt C wędruje po półprostej BM i w zależności od jego położenia otrzymujemy różne trójkąty ABC, i w konsekwencji NMQ. Nie jestem jednak tak obcykany, żeby udowodnić, że za każdym razem NMQ jest równoboczny. Przypuszczam, że nie jest to zadanko dla niewinnych dziatek.

sushi_ gg6397228: pewno jakaś olimpiada

PW: To nieprawda, że ΔABC jest równoboczny, i nie da się tego udowodnić przy założeniach zadania. Równie dobrze trójkąt o boku AB i kątach 60°, 40°, 80° spełnia warunki postawione w zadaniu.

PW: Teraz to moje wypowiedzi są nie na temat , wygląda że polemizuję z samym sobą i moje alter ego ma inną płeć, ale nich będzie (jestem przeziębiony i to pewnie efekt gorączki).

Piotr: przeziebiony w taki upal ? za duzo lodow

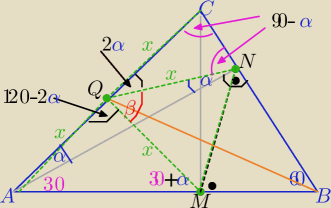Eta: β=60^o oraz trójkąt NMQ jest równoramienny o ramionach długości x zatem jest trójkątem równobocznym Poprzednich komentarzy nie chce mi się już pisać: PW ...pasuje teraz

Eta: PW ...życzę dużo zdrówka

PW: Dziękuję, wczoraj byłem do niczego. Nie zauważyłem, że kluczowe dla rozwiązania jest spostrzeżenie, że w trójkącie prostokątnym odcinek łączący wierzchołek kąta prostego ze środkiem przeciwprostokątnej ma długość równą połowie przeciwprostokątnej: |QN| = |QC| = x. I dlatego otrzymujesz tytuł Dobrej i Obcykanej w Matmie 252955