zadanie 22 Alunia: Mając odcinki o długościach: 1, a i b, skonstruuj odcinek o długości x=a/b. Mając odcinki o długościach a i b, gdzie a>b, skonstruuj odcinek o długości x= (a²−b²) / (a+2b). Nie mam pojęcia jak to zadanie zrobić, proszę, pomóżcie

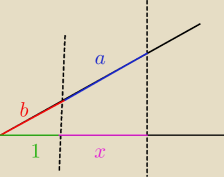
Janek191: cz. I Z tw. Talesa mamy

b		1		a
	=		⇒ b*x = a*1 = a ⇒ x =
a		x		b

Proste ( linie przerywane ) są równoległe

diana7: 2. Bierzemy sobie trójkąt ABC o kącie prostym A, w którym AC=b i BC=a. Po jego zewnętrznej stronie budujemy kwadrat ABDE. Jeśli uda nam się znaleźć prostokąt o polu a²−b² (równym polu ABDE) i jednym z boków równym a+2b to koniec. Przedłużmy AC poza A i zaznaczmy na tym przedłużeniu taki punkt F, że AF=a+2b. Następnie narysujmy prostą równoległą do FB przechodzącą przez E. Prosta ta przecina AB w jakimś punkcie T, no i F, A, T są trzema wierzchołkami szukanego prostokąta. Może jest jakieś prostsze rozwiązanie .