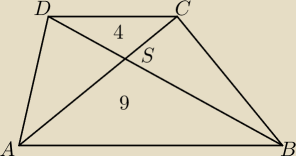
zadanie 13 Alunia: Przekątne trapezu ABCD przecinają się w punkcie S. Pole trójkąta ABS wynosi 9, a pola trójkąta CDS jest równe 4. Wysokość trapezu jest równa 10. Oblicz pole trapezu.

Bogdan: Wysokość nie jest potrzebna. Pole trapezu P = (√9 + √4)² = ...

Alunia: skąd wziąłeś to obliczenie?

5-latek: Alu . Masz to w ksiazce i nawet wyprowadzone dlaczego tak . Wiec zobacz

pigor: ...., lub: niech a>b − długości podstaw danego trapezu, wtedy P_t=¹₂(a+b)*10=5(a+b)=? − szukane pole trapezu ABCD, to z warunków zadania i tw. o polach Δ podobnych, tu ΔABS∼ΔCDS (cecha kkk) ⇒ ⇒ h₁+h₂= 3k+2k=10 ⇒ k=2 ⇒ h₁=6 i h₂=4 − dl. wysokości ΔABS i ΔCDS odpowiednio, to ¹₂a*6=9 i ¹₂b*4=4 ⇒ a=3 i b=2 , zatem P_t= 5(2+3)= 5*5= 25 j² − szukane pole trapezu ABCD. ...

Bogdan:

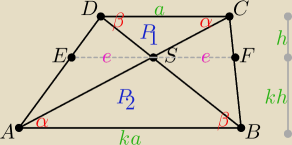
	P2
Trójkąty ABS i CDS są podobne w skali k, stąd		= k2 ⇒ P2 = k2P1
	P1

Łatwo jest wykazać, że pola trójkątów ASD i BSD są równe, oznaczam to pole P₃

	ka		kh + h		ka
Trójkąty ABD i ESD są podobne:		=		⇒ e =
	e		h		k + 1

	1		1		1
PASD = PBSC = P3 =		eh +		e*kh =		eh(1 + k) =
	2		2		2

	1		ka		P3
=		*		*h(1 + k) = U{1}[2}kah = k*P1 ⇒ k =
	2		k + 1		P1

P2		P2		P32
	= k2 ⇒		=		⇒ P32 = P1*P2
P1		P1		P12

Pole trapezu P_T = P₁ + P₂ + 2P₃ = P₁ + P₂ + 2√P₁P₂ = (√P₁ + √P₂)²

Bogdan: Zamiast { wpisałem [, poprawiam ten fragment:

	1		P3
P3 = ... =		kah = k*P1 ⇒ k =
	2		P1

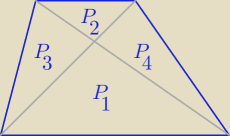
Eta: 2 sposób: P(tr)=(k+1)²*P₂ , k >0 −−skala podobieństwa trójkątów o polach P₁ i P₂ P₃=P₄=k*P₂ P₁=k²*P₂ P(tr)= P₁+p₃+P₄+P₂= k²*p₂+2k*p₂+P₂= (k²+2k+1)*P₂= (k+1)²*P₂

P1		9		3
	=k2 ⇒ k2=		⇒ k=
P2		4		2

	3
P(tr)=(		+1)2*4= ......... = 25 [j2]
	2

Alunia: Dziękuję bardzo wszystkim za rozwiąznia Bardzo mi się przydały