Geometria matstus: Na bokach AB, BC oraz AC trójkąta ABC, punkty a,b,c są obrane odpowiednio tak, że Ac= Ab, Ba= Bc oraz Ca=Cb. Udowodnij, że punkty a,b,c są punktami styczności z okręgiem wpisanym w ten trójkąt.Jakaś wskazówka !

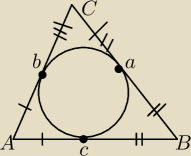
Michał: Założenie: Trójkat ABC − rożnoboczny Ac = Ab Ba = Bc Ca = Cb Teza: a, b,c punkty styczności z okręgiem wpisanym w trójkąt ABC

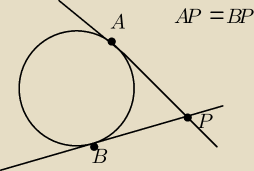
Michał: Dowód przeprowadziłbym na podstawie twierdzenia o odcinkach stycznych tj.: Odcinki dwóch stycznych, poprowadzonych do okręguu z punktu którego odległość od srodka okregu jest większa niż promień − wyznaczone przez ten punkt i odpowiednie pkt styczności − mają tą samą długość.

kama: Jeśli się nie mylę to jak mamy koło wpisane w figurę to odległości z jednego wierzchołka do punktu styczności z tym kołem są takie same. Niby posługując się samymi założeniami można to udowodnić. Tylko nie jestem pewna jak to zapisać.