HELP
Ania:
Wyznacz równanie okręgu wpisanego w kwadrat ABCD , gdzie A = (1,1) i C = (5,3) .
Tak mi wychodzi (x−3)
2+(y−2)=5 a w odpowiedzi jest inny promień

7 cze 21:50
Lukas:

Połowa przekątnej nie jest długością promienia.. długość promienia to połowa boku..
7 cze 21:52
Ania:
A opisanego ?
7 cze 21:53
Lukas:
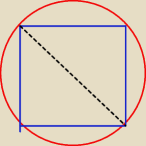
7 cze 21:59
Mila:

A = (1,1) i C = (5,3) .
|AC|− przekątna
środek okręgu:
|AC|=
√42+22=
√20=2
√5
R=
√5 − promień okręgu opisanego na kwadracie
obliczamy a
d=2
√5
d=a
√2⇔a
√2=2
√5 /*
√2
2*a=2
√10
a=
√10
| | 5 | |
(x−3)2+(y−2)2= |
| równanie okręgu wpisanego w ten kwadrat |
| | 2 | |
=============================================
7 cze 22:22
Ania:
Dziękuję, zrozumiałam już po wcześniejszych rysunkach

7 cze 22:23

 Połowa przekątnej nie jest długością promienia.. długość promienia to połowa boku..
Połowa przekątnej nie jest długością promienia.. długość promienia to połowa boku..

 A = (1,1) i C = (5,3) .
|AC|− przekątna
środek okręgu:
A = (1,1) i C = (5,3) .
|AC|− przekątna
środek okręgu:
