Wykres funkcji kwadratowej Proxi: Cześć, prosiłbym o pomoc przy tym zadaniu: Narysuj wykres funkcji f(x)= −|x2+4x|+1. Określ liczbę rozwiązań równania f(x)=m w zależności od wartości parametru m.

Piotr 10: Najlepiej to wpierw wyłączyć minus przed nawias, a więc: f(x) = − ( Ix²+4xI − 1 ) Teraz rysujemy wykres y = x² + 4x Następnie robimy Wb_OX ( to co jest na górze pozostawiamy bez zmian, a to co jest poniżej osi X odibjamy względem niej ) Następnie translacja o wektor u^→=[ 0 ; − 1 ] A na końcu symetria względem osi OX ( S_OX ) Ja to bym to tak robił

Proxi: Dzięki, narysowałem wykres ale teraz muszę jeszcze określicz liczbę rozwiązań równania f(x)=m w zależności od wartości parametru m

Piotr 10: To tak: Rysujesz sobie kilka prostych ( tylko tak lekko je rysuj najlepiej ołówkiem lub innym kolorem) równoległych do osi OX ( tak na oko ) . I teraz liczba przecięc z tą prostą oznacza liczbę rozwiązań

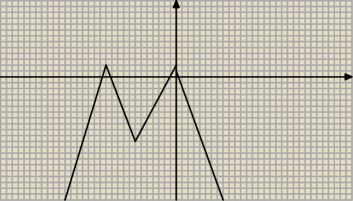
Proxi: Wyszedł mi taki wykres. Czyli dla m∊R rozwiązaia są 4?

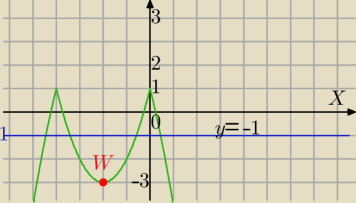
Mila: f(x) = −( Ix²+4xI − 1 ) g(x)=x²+4x

	−4
xw=		=−2
	2

g(−2)=4+4*(−2)=−4 |g(−2)|=4 |g(−2)|−1=3 Po przekształceniach (−2,−3) wsp. wierzchołka 1) m<−3 dwa rozwiązania 2)m=−3 3 rozwiązania 3) m∊(−3,1) cztery rozwiązania ( przykład dla y=−1) 4) m=1 dwa rozwiązania 5) m>1 brak rozwiązań