planimetria dżasta: długości ramion trapezu wynoszą 5 cm i 2 √5 a długości podstaw wynoszą 3 cm i 8 cm. Oblicz pole tego trapezu.

dżasta: ?

pigor: ..., np.tak : P_t= ¹₂(8+3)h= ¹¹₂h = ?, no to niech x − rzut ramienia długości np. 2√5 na dłuższą podstawę AB, to (*) h²= (2√5)²−x²= 5²−(8−3−x)² ⇒ 20−x²= 25−(5−x)² ⇔ ⇔ (5−x)²−x²= −5 ⇔ (5−2x)*5= −5 ⇔ 5−2x= −1 ⇔ x=2, zatem z (*) h²= 4*5− 4 = 16 ⇒ h=4, a więc P_t= ¹¹₂*4 = 22 cm². ...

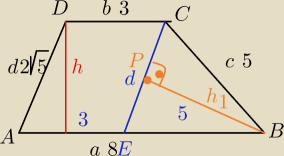
Mila: ΔCEB jest Δ równoramiennym CP=√5 W ΔBPC: h₁²+|PC|²=c² h₁²=25−5=20 h₁=√20 h₁=2√5

	1		1
PΔBEC=		*|EC|*h1=		*2√5*2√5=10
	2		2

Obliczamy pole tego trójkąta drugim sposobem

	1
PΔBEC=		*|EB|*h
	2

	1
10=		*5*h
	2

h=4− wysokość trapezu Teraz dokończ zadanie. ===============

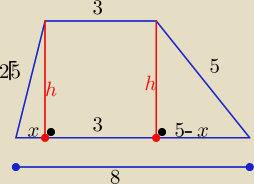
Eta: x∊(0,5) (2√5)²−x²=h² i 5²−(5−x)²=h² to: 20−x²= 25−(5−x)² ⇒ ....x=2 h= √5²−3²= 4

	3+8
P=		*4=..... = 22 cm2
	2

Mila: Zobaczymy co na to powie dżasta?

Eta: Przepisze i podkreśli odp: ==============================

Mila: Myślę, że nam podziękuje, bo w przeciwnym przypadku.....

dżasta: oba rozwiązania rozumiem do połowy. jeszcze nie przepisałam, bo myślę

dżasta: bardzo dziękuję!: )

Mila: Pomyśl, a na pewno zrozumiesz, możesz pytać, ale tam tylo pole Δ i tw. Pitagorasa, to chyba umiesz?