planimetria Miniś: Witam, piszę jeszcze raz, bo zadanie zniknęło gdzieś w dole Bardzo proszę o pomoc, to dość pilne 1. W trójkąt o ramionach długości 10 i kącie między ramionami 120stopni wpisano okrąg. Oblicz długość promienia tego okręgu 2. Wykaż, że trójkąt o bokach długości 4, 3√3,2√5 jest ostrokątny Domyślam się, że trzeba użyć tu twierdzenia cos i wyliczyć miary kątów, tak ? Tu mam lekki problem z uproszczeniem tego wszystkiego, bo wychodzi: np. dla boku 4 42=(3√2)2*(2√5)2−2*3√2*2√5*cos(np.α) 16=18*20−12√10*cosα i co dalej ? 3. W trójkącie ABC długość boku AB=8 oraz kąt ACB=45stopni i kąt ABC=30stopni. Oblicz długość promienia R okręgu opisanego na tym trójkącie i długość najdłuższego boku trójkąta. R policzyłem z tw sin, wyszło: R=4√2 −−> dobrze ? Potem obliczyłem bok AC też z tego twierdzenia, wyszło też 4√2, pytanie tylko jak policzyć 3 bok, bo kąt naprzeciw tego boku=105 stopni(mam użyć wzorów redukcyjnych ?) i policzyć z tw cos ? 4. W czworokącie ABCD: AD=4 CD=6 oraz kąt CDA=2*kątABC. Oblicz długość przekątnej AC, jeżeli wiadomo, że na tym czworokącie można opisać okrąg. I tu ściana, nie mam żadnego pomysłu, zrobiłem obrazek, doszedłem, że 4+6=a+b(dwa pozostałe boki) i wyznaczyłem podane kąty jako α i 2α, ale co dalej ?

Gośka: w zadaniu 1 można np tak rysujesz wysokość która dzieli kąt na pół i z sin60 wyliczasz podstawę, a potem z cos60

	1
wysokość. Liczysz pole ze wzoru P=		ah a potem jak już masz pole to liczysz je ze wzory
	2

	1
P=rp gdzie r to promień okręgu wpisanego, zaś p=		(a+b+c)
	2

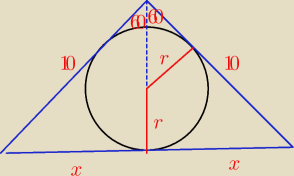Janek191: Mamy

x		√3
	= sin 60o =
10		2

x = 5√3 Pole Δ

	√3
P = 0,5 *102*sin 120o = 50*cos 30o = 50*		= 25 √3
	2

Obwód Δ L = 2*10 + 2 x = 20 + 10√3 Korzystamy z wzoru P = 0,5 L*r 2 P = L*r

	2 P		50 √3		5√3
r =		=		=		= dokończ
	L		20 + 10√3		2 + √3

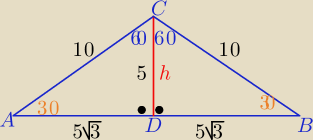Eta: 1/ P=r*p, r −− dł. promienia okręgu wpisanego w trójkąt p −− połowa długości obwodu trójkąta

	1
P=		*|AB|*h =....... p=..........
	2

	P
r=		=...
	p

2/ a,b,c −− dł. boków trójkąta , c −−− dł. boku najdłuższego Jeżeli a²+b²=c² −−−− to trójkąt jest prostokątny Jeżeli a²+b²>c² −−− to trójkąt jest ostrokątny Jeżeli a²+b²< c² −−− to trójkąt jest rozwartokątny zatem............

Eta: Znów "sypnęło" ......... jak zeszłorocznym śniegiem Zostawiam resztę zadań dla ..........

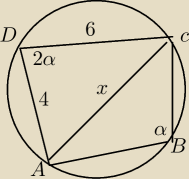Gośka: Z właśności czworokąta wpisanego mamy że 2α+α=180^o czyli α=60^o Potez z tw cosinusów x²=4²+6²−4*6*c0s(120^o)

Miniś: Dziękuje bardzo za pomoc Janek191: Czy r powinno wyjść 7 ? Bo nie wiem czy dobrze niewymierność usunąłem Gośka: cos120stopni przejdzie w sin30stopni, czyli 1/2 i wyjdzie razem: 4√7 Poza tym jak piszecie dzielenie przez kreskę ułamkową, bo mi nie wychodzi Jeszcze tylko to zadanie i pójdę spać szczęśliwy dzieki wam W trójkącie ABC długość boku AB=8 oraz kąt ACB=45stopni i kąt ABC=30stopni. Oblicz długość promienia R okręgu opisanego na tym trójkącie i długość najdłuższego boku trójkąta.

Eta:

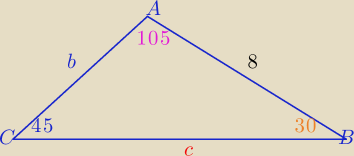
	8
z tw. sinusów :		=2R ⇒ R=........
	sin45o

	c
		=2R ⇒ c=........
	sin105o

sin105^o= sin(60^o+45^o)=......

Miniś: R wyszło mi 4√2. A tu sin105= sin(60+45)= to przejdzie w cos45 czyli √2/2 ? Jak się to robi, bo umiem, ale dla kątów 90, 180, 270, 360

Janek191: r = 10√3 − 15 Tak jak obliczyła Mila

Miniś: a możesz mi rozpisać to ^5√3_22+√3 ?

Mila:

5√3		2−√3		5√3*(2−√3)
	*		=		=
2+√3		2−√3		22−(√3)2)

	10√3−15
=		=10√3−15
	4−3

Miniś: Dziękuje, już rozumiem

Mila: