Oblicz Całkę
Asia: Oblicz całkę
Proszę o pomoc, z góry dziękuję
5 cze 17:54
Asia: proszę, bardzo mi zależy na czyjejś pomocy

5 cze 17:58
Janek191:
Napisz porządnie, bo nie wiadomo co tam jest

5 cze 18:00
Godzio:
Pewnie granice, ale kto to wie

5 cze 18:00
Mila:
(2x) jest wykładnikiem?
Granice mogą być od (−2) do 3
5 cze 18:01
Asia:
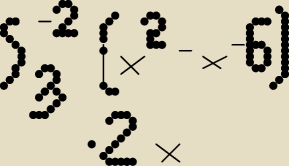
∫
5 cze 18:06
Godzio:
Tak? (−2 i 3 to granice całkowania)
5 cze 18:07
Asia: pierwsze to całka − ∫
5 cze 18:07
Asia: −2 jest na gorze tez a 3 wlasnie na dole

ciezko tu napisac poprawnie przyklad, przepraszam

5 cze 18:08
Janek191:
Całka z jakiej funkcji ?
5 cze 18:08
Asia: od −2 do 3 chyba, wlasnie nie rozumiem tego zapisu
5 cze 18:10
Asia: bardzo proszę o pomoc

5 cze 18:14
Asia: czy ktoś potrafi pomóc mi w rozwiązaniu? bardzo mi na tym zależy
5 cze 18:21
Godzio:
| | x2 − x−6 | | x | | 1 | | x2 | | 1 | x−6 | |
∫ |
| dx = ∫( |
| − |
| x−7)dx = |
| − |
|
| = |
| | 2x | | 2 | | 2 | | 4 | | 2 | −6 | |
Podstaw sobie teraz granice
5 cze 18:22
zawodus: Napisz to dobrze, to pomożemy

5 cze 18:22
Janek191:
∫ (x2 − x−6)*2 x dx ?
5 cze 18:23
Asia: tak i obok symbolu całki czyli ∫ na gorze jest −2 a na dole 3
5 cze 18:24
Janek191:
Trzeba wymnożyć przez 2 x i będzie bardzo łatwa całka

5 cze 18:27
Asia: czyli te − 2 i 3 przy calce nie ma nic do znaczenia ?
5 cze 18:28
Janek191:
= ∫ ( 2 x3 − x−5 ) dx =
5 cze 18:28
Janek191:
Ma , ale najpierw oblicz całkę nieoznaczoną

5 cze 18:29
Asia: no dobrze, a dlaczego zniklo z nawiasu jeszcze −6 ?
5 cze 18:29
Janek191:
Pomyliłem się

Ma być
= ∫ (2 x
3 − 2 x
−5) dx =
5 cze 18:30
Janek191:
x−6*x = x − 6 + 1 = x−5
5 cze 18:31
Asia: | | 1 | | 1 | |
wyszlo mi = |
| x4 − |
| x−4 |
| | 2 | | 4 | |
5 cze 18:32
Asia: acha, to ja do tamtego liczylam, a powiedz mi proszę czy do tamtego dobrze obliczylam całkę ?
5 cze 18:33
Asia: i to już jest koniec przykładu

?
5 cze 18:37
Janek191:
Tak.
Policz jeszcze raz dla
∫ (2 x3 − 2 x−5) dx
a następnie oblicz całkę oznaczoną w podanych granicach
5 cze 18:40
Janek191:
Uważaj na znaki

5 cze 18:42



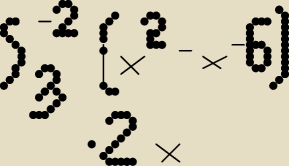 ∫
∫
 ciezko tu napisac poprawnie przyklad, przepraszam
ciezko tu napisac poprawnie przyklad, przepraszam





 Ma być
= ∫ (2 x3 − 2 x−5) dx =
Ma być
= ∫ (2 x3 − 2 x−5) dx =
 ?
?
