zadAnie z ostrosłupów pilne!!
łaml: Krawędź podstawy ostroslupa prawidłowego trójkątnego ma długość 9cm zaś krawędź boczna 7cm.
Oblicz sinus kata nachylenia krawędzi bocznej do płaszczyzny podstawy.
5 cze 11:26
J:
| | H | |
Policz 2/3 wysokości podstawy. Potem H − wysokość ostrosłupa , sinα = |
| |
| | 7 | |
5 cze 11:32
łaml: A mógłbyś to zrobić?

5 cze 11:33
J:
A czego nie wiesz ? .... Jaki jest wzór na wysokość trójkąta równobocznego o boku a ?
5 cze 11:37
Bogdan:
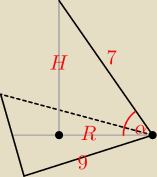
Niepotrzebna jest wysokość podstawy.
H obliczamy korzystając z tw. Pitagorasa.
5 cze 11:39
J: | | 2 | |
Potrzebne są |
| wysokości podstawy. |
| | 3 | |
5 cze 11:43
Bogdan:
Warto pamiętać zależności na długość promienia okręgu opisanego na trójkącie
| | 1 | |
równobocznym R = |
| a√3 oraz na długość promienia okręgu wpisanego |
| | 3 | |
| | 1 | |
w ten trójkąt r = |
| a√3, nie ma wtedy potrzeby obliczać długości wysokości |
| | 3 | |
| | 1 | |
trójkąta równobocznego h = |
| a√3 i potem wykonywać kolejne obliczenie |
| | 2 | |
| | 2 | | 1 | |
R = |
| h albo r = |
| h. |
| | 3 | | 3 | |
Czas podczas sprawdzianu, egzaminu jest bardzo cenny.
5 cze 11:56
J:
| | 1 | |
r = |
| a √3 ..  |
| | 6 | |
5 cze 12:01
Bogdan:
Dziękuję
J za zauważenie chochlika,
| | 1 | | 1 | |
r = |
| R = |
| √3  |
| | 2 | | 6 | |
5 cze 13:20
J: Takie literówki zdarzają sie każdemu ...

5 cze 13:22




