F. kwadratowa zadania - optymalizacyjne Mat-fiz z nazwy : Siatką drucianą o długości 60m należy ogrodzić prostokątny plac przylegający jednym bokiem do muru. Jakie wymiary powinien mieć plac, aby jego pole powierzchni było największe?

Mat-fiz z nazwy : Na razie mam coś takiego 2x + y = 60 y = 60 −2x P = 60x − 2x²

sushi_ gg6397228: i teraz liczysz wierzchołek

Mat-fiz z nazwy : a dziedzina ? No ok Xw = 60 / 4 Xw = 15 f(Xw) = 60 * 15 − 2 * (15)² Yw = 450 −₋

Eta: y=60−2x , x∊( 0,30) x_max= 15 m to y_max= 60−2*15= 30m

sushi_ gg6397228: 60x−2x²= −2x²+60x= −2x(x−30) wiec widac, że x_w= 15, pole (y_w)= 450 x,y ∊ (0; 60)

Eta: ?

Mat-fiz z nazwy : dobra poprawka y = 30 x = 15 tylko pytanie bo tu tzra było jeszcze (chyba ) dziedzinę wyznaczyć i to średnio pamiętam

Mat-fiz z nazwy : Nie czytałem waszych wypowiedzi przed swoim przed przed ostatnim postem . x∊( 0,30) to jest dziedzina ? jak to ? się liczy

Eta: P(x)=x(60−2x) D: x∊(0,30)

pigor: ..., P(x)=x(60−2x)= −2x(x−30) i x∊(0;30) ⇒ ⇒ P_największe= P(¹₂(0+30)= P(x=15), a wtedy y=60−2*15= 30, zatem odp. plac powinien mieć wymiary 15m x 30m . ...

Eta: y=60−2x x>0 i y>0 ⇒ 60−2x>0 ⇒ x.........

Mat-fiz z nazwy : chodzi , że ... x> 0 60 − 2x >0 x> 30 to z tego wynika ?

Mat-fiz z nazwy : dobra dzięki jak by co to mogę tu inne zadania wrzucać ?

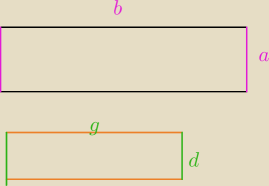
Mat-fiz z nazwy : prostokąt ma boki długości a cm i b cm . Bok a powiększamy o x cm , zaś bok b zmniejszamy o x cm. Dla jakiej wartości x pole nowego prostokąta będzie największa . ( obrazek jest mój ) Na początku napiszę to co mam g = b −x d = a + x P = ( a + x )*( b− x ) No i tu się zaciąłem

sushi_ gg6397228: pole zawsze największe jest dla kwadratu, jak masz same literki, to nie wiele się policzy liczysz tak jak zadanie "1" zmienna jest "x", stałe to "a i b"

sushi_ gg6397228: masz miejsca zerowe x₁= −a x₂= b

	b−a
wiec wierzchołek xw jest po środku xw=
	2

Mat-fiz z nazwy : Dziedzina ?