przebieg zmienności funkcji kk: Zbadaj przebieg zmienności funkcji. Narysuj wykres i sporządź tabelkę

	4−x2
f(x)
	x2−1

kk: pomocyyy

Krzysiek: i pewnie nic z kilku/nastu podpunktów nie zrobiłeś? i jeszcze na jutro to masz?

sushi_ gg6397228: I ZADALI 5 MINUT TEMU

kk: jakiś problem bo nie rozumie?

WueR: Problem jest w tym, ze nikt Ci tu gotowca nie zaoferuje. Pisz z czym >konkretnie< masz problem, to ktos wtedy na pewno pomoze, ale nie licz, ze ktos zbada funkcje za Ciebie od "deski do deski".

kk: Krzysiek aż tak tępa nie jestem i ZROBIŁAM wyobraź to sobie! ale nie umiem zrobić ekstremum i monotonicznośći, tabelki i wykresu!

kk: z tym co napisałam

kk: a nie zadali 5 SEKUND TEMU SUSHI

sushi_ gg6397228: to zapisuj 1−wszą pochodną

kk:

−6x
(x2−1)2

kk: teraz ma być ekstremum czyli do 0 przyrównuję i nie wiem jak to ma być

WueR:

f(x)
	= 0 ⇔ f(x) = 0 ∧ g(x) ≠ 0
g(x)

sushi_ gg6397228: −6x=0 x=...

kk:

	−6x
f'(x)=0 ⇔		=0
	x2−1)2

−6x=0 x=0 dobrze?

sushi_ gg6397228: i teraz badanie znaku w sasiedztwie "0"

kk: f'(x) >0 f"(x)<0 nie umiem tego

sushi_ gg6397228: z lewej strony "miejsca zerowego" podstawiasz liczbę trochę mniejsza od zera np "−0,5" i sprawdzasz jaki jest znak; to samo z prawej strony

kk: to chyba nie o to mi chodzi, chce wyznaczyc przedziały monotoniczności a nie granice

Bogdan:

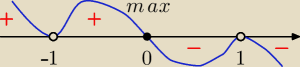
	−6x
f'x) =		i x≠−1 i x≠1
	(x − 1)2 (x + 1)2

Monotoniczność: f↗ dla x∊(−∞, −1), (−1, 0) f↘ dla x∊(0, 1), (1, +∞) Ekstremum: f_max = f(0) = −4

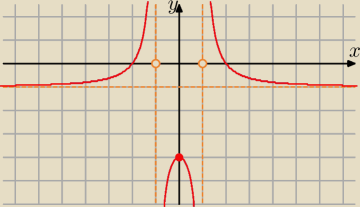
Bogdan: To jest wykres funkcji f(x), są dwie asymptoty pionowe: x = −1, x = 1 oraz asymptota pozioma y = −1