okręgi okręgi: Środki czterech okręgów o promieniu r=6 znajdują się w wierzchołkach kwadratku o boku długości a=6. Znajdź pole wspólnej części tych czterech kół.

okręgi:

daga: pomoze ktos Środki czterech okręgów o promieniu r=6 znajdują się w wierzchołkach kwadratku o boku długości a=6. Znajdź pole wspólnej części tych czterech kół.

Zbronek: P=36(1−√3)+12π

Zbronek:

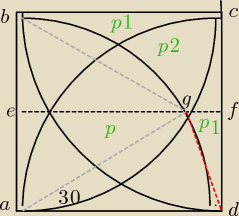
	6√3		6√3
Δbag −równoboczny⇒|eg|=		⇒|gf|=6−		=6−3√3
	2		2

	1		1		9
PΔgfd=		|gf|*3=		(6−3√3)*3=		(2−√3)
	2		2		2

	1
Pwycinka.agd=		*36π=3π
	12

	1		1
PΔagd=		*6*		*6=9
	2		2

P_{cześci.wycin.agd.odp.cięciwie.gd}=3π−9

1		9
	p1=PΔgfd−Pcześci.wycin.agd.odp.cięciwie.gd=		(2−√3)−3π+9
2		2

p1=9(2−√3)−6π+18=36−9√3−6π 2p₁+p₂=36−9π p₂=36−9π−2p₁=36−9π−2(36−9√3−6π)=3π+18√3−36 p=36−4p₁−4p₂=36−4(36−9√3−6π)−4(3π+18√3−36)=36(1−√3)+12π

daga: o dzieki wielkie za rozwiazanie

ewa: Pcześci.wycin.agd.odp.cięciwie.gd=3π−91 wytłumaczy mi to ktos?

BiebrzaFun : P_{cześci.wycin.agd.odp.cięciwie.gd}=3π−9 P_wycinka.agd=3π P_Δagd=9 https://matematykaszkolna.pl/strona/474.html rysunek nie wyszedł może dokładnie,czerwona przerywana dzieli wycinek koła na Δagd i cześć wycinka agd odp cięciwie gd