okręgi ada: a) Środki czterech okręgów o promieniu r=6 znajdują się w wierzchołkach kwadratu o boku długości a=12. Oblicz promień okregu stycznego do wszystkich czterech okręgow. (rozpatrz dwa przypadki) b) Trzy okregi o promieniu równym r=6 są parami styczne. Oblicz promień okregu stycznego do wszystkich trzech okręgów. (rozpatrz dwa przypadki)

ada: pomoze ktos

ada: bo nie wiem jak sie zabrac wogole do tego

ada: choc jeden przyklad...... plis.....

AROB: pomogę

psotka: Wiem , tylko nie chce mi się rysować Witaj AROB zostawiam Tobie ( rysowanie

psotka: ok Tak jak przewidziane

ada: bede ogromnie wdzieczna

psotka:

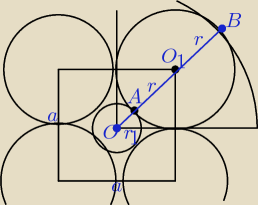
AROB: a) Trudno mi narysować cały rysunek, zrobię fragment. r= 6 cm, a = 12 cm r₁ = IOAI = ? R= IOBI = ? IOO₁I = a√2 (przekątna kwadratu)

	1
r1 + r =		* a√2
	2

	1
r1 + 6 =		* 12√2 ⇒ r1 = 6√2 − 6 = 6(√2 − 1)[cm]
	2

R = IOBI = r₁ + 2r = 6√2 − 6 + 12 = 6√2 + 6 = 6(√2 + 6) [cm]

psotka: poprawimy chochlika R= 6(√2+1) cm

ada: i to są rozpatrzone dwa przypadki w tym a) czy tylko jeden

AROB: Jasne Eta, pomyłka w przepisywaniu. Dzięki. Witaj psotko

ada: aha.... juz wiem oba

AROB: To są dwa przypadki do a) : pierwszy to r₁, a drugi to R.

godzio187: 2 1− stycznie wewnętrznie 2−stycznie zewnętrznie

ada: Dziękuje a tego b) nie podjąl by sie ktos moze

AROB: No godzio187, ruszaj do zad.2. Tak ładnie rysujesz przecież. Witaj!

psotka: Witam godzio dawaj zad2/ trójkat równoboczny itd..... , dasz radę , wierzę w Ciebie Pomóż Adzie..

psotka:

godzio187: moge spróbować

psotka: to ja idę na herbatkę

AROB: No to robimy razem.

psotka: Ale ja herbatkę a nie zadanie! Zad. robi godzio

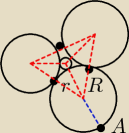
godzio187: Rysunku zabardzo nie umiem to bd mówić co czym jest r₁−promien malego okregu r−promien wiekszego okregu R−promien duzego okregu 2r=12

	2	12√3
r+r1=			=4√3
	3	2

r₁=4√3−6=2(2√3−3) dobrze ? jak tak to robie dalej

godzio187: R=r₁+2r=4√3−6+12=4√3+6

godzio187: tylko nie wiem czy to są wysokości i

ada: czyli rysunek prawie jak wyzej tylko z trojkatem.... oki to bede wiedziala co do oznaczen

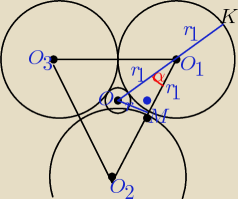
AROB: Dane: r₁ = 6 cm, obl. r, R=IOKI Z ΔOMO₁ obliczam r (promień najmniejszego okręgu, stycznego do 3 okręgów, leżącego między nimi).

	r1
		= cosα
	IOO1I

6
	= cos300
r+6

6		√3
	=
r+6		2

√3(r+6) = 12 r√3 + 6√3 = 12

	12 − 6√3		6(2−√3) *√3
r√3 = 12 − 6√3 ⇒ r =		=		= 2√3(2 − √3) =
	√3		3

= 4√3 − 6 = 2(2√3 − 3)[cm] R =IOKI − to promień okręgu obejmującego 3 styczne okręgi (brak go na rysunku) R = 2r₁ + r = 12 + 2(2√3 − 3) = 12 + 4√3 − 6 = 6 + 4√3 = 2(3 + 2√3)[cm]

godzio187: czyli dobrze wyszło

AROB: Znakomicie!

godzio187:

	2
ale można było założyć że r1+r=		h ?
	3

ada: bardzo dziekuje wszystkim za pomoc

AROB:

AROB: Tak godzio187 , ponieważ trójkąt O₁O₂O₃ jest równoboczny, a jego wysokości w takim stosunku się przecinają.

AROB: Zmykam Dobranoc Eta i godzio187.

godzio187: dobranoc