analityczna Lukas: x²+y²−8x+12= 0 styczne do okręgu przechodzą przez początek układu współ Oblicz pole figury ograniczonej stycznymi i łukiem okręgu wyznaczonym przez punkty styczności. . Punkty styczności wyszły A=(3,−√3) B=(3,√3) Jak dalej obliczyć to pole ?

Janek191: Obliczyć pole czworokąta ( deltoid ) i pole wycinka kołowego i wykonać odejmowanie.

Lukas: Ok, dzięki. Wyjdzie coś z π ? Mogę tak zostawić ?

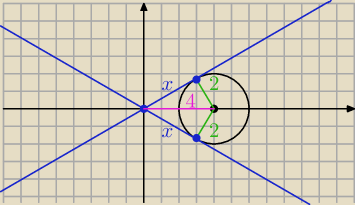
Saizou : x²−8x+16−16+y²+12=0 (x−4)²+y²=4 S(4:0) r=2 d=r y=ax ax−y=0

	l4a+(−1)*0
2=
	√a2+1

2√a²+1=l4al 4a²+4=16a² 4=12a²

	1
a2=
	3

	√3		√3
a=		lub a=−
	3		3

x²+2²=4² x²=12 x=2√3

	1
Pf=2*		*2x=4√3
	2

Lukas: ehh... Dzięki....

Janek191:

	4
P = 4√3 −		π
	3

Saizou : nie doczytałem trzeba jeszcze odjąć pole wycinka

Lukas: Też mi tak wyszło i tak zostawić ?

Saizou : a co chcesz z tym zrobić ?

Lukas: Teraz już nic.

Saizou : pokaż jeszcze jak obliczyłeś ką przy czarnej kropce

Lukas: Trójkąt jest prostokątny więc policzyłem sinusa i potem wycinek koła i po zadaniu.

Saizou :

Lukas:

Saizou : bo można też sobie utrudnić życie

Lukas: Tzn ? z twierdzenia cosinusów o to Ci chodzi ?

Saizou : na przykład

	√3
najszybciej chyba wiedzieć że tgα=		(kąt nachylenia prostej do osi x)→α=30o
	3

Saizou : a jednak szybciej z cosinusa : bo nie potrzeba wtedy stycznych

Lukas: ale miałem w poleceniu też wyznaczyć styczne specjalnie tak sformułowałem treść zadnia żeby nikt nie wrzucał mi rozwiązania tylko dał wskazówkę

Saizou : spoko, ale i tak rozwiązałem, prawie

Lukas: Dziękuję.