Bardzo proszę o pomoc, rysunek również mile widziany:) Wojtek: ∬min(x,y) dxdy, D=[0,1] x [0,2] Obliczyć całkę podwójną po wskazanych obszarach. Uwaga. Symbol min(a,b) oznacza mniejszą spośród liczb a,b,

Krzysiek: rozbij na sumę dwóch całek. pierwsza to będzie: ∫₀¹∫₀^xydydx

Wojtek: mógłbym prosić bardziej szczegółowo? bo dalej nie wiem jak to ugryźć

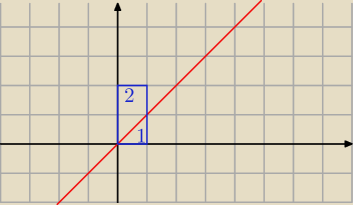
Krzysiek: rozbijasz całkę na dwa obszary 1 i 2. bo na obszarze 1. min(x,y)=y a na obszarze 2. min(x,y)=x i wystarczy określić granice całkowania

Wojtek: mógłbyś jeszcze mi napisać tą sumę dwóch całek, bo już prawie łapie o co chodzi, ale nie chce zrobić babola

Krzysiek: to napisz jak ci się wydaję to sprawdzę.

Wojtek: Już trochę zgłupiałem z tym, coś takiego? to min(x,y) mi miesza, bo całka po prostokącie to raczej prosta sprawa się wydaje. Ogólnie to jestem w trakcie przyswajania materiału z calek podwójnych, a ten przykład muszę zrobić jutro na zajęcia, dlatego proszę o pomoc ∫0¹∫0^x ydydx + ∫1²∫1^y xdydx

Krzysiek: źle ta druga całka... przecież granice całkowania dla 'x' to [0,1] nic się nie zmieniło.. a granice całkowania dla 'y' to [x,2] a funkcja min(x,y) dla obszaru 2 czyli nad prostą y=x czyli y≥x więc masz min(x,y)=x więc to jest dobrze.

Wojtek: Czy coś takiego? ∫0¹∫0^x ydydx + ∫0¹∫0^y xdydx

Wojtek: Okej już doszedłem jakie całki po podzieleniu tego obszaru. ∫0¹∫0^x ydydx + ∫0¹∫x² xdydx . Tylko mógłbyś napisać dlaczego akurat taką prostą dzielimy ten obszar? Dzięki za pomoc do tej pory

Krzysiek: szukasz min(x,y) więc rysujesz prostą y=x, nad prostą masz y≥x( czyli dla każdego 'x' y jest większe, więc min(x,y)=x ) a pod prostą y≤x .i wtedy min(x,y)=y

Wojtek: Wszystko już jasne, dzięki piękne