Rozpatrujemy trapezu równoramienne, w których jedna z podstaw jest 3 razy dłuższ Cersei: Rozpatrujemy trapezu równoramienne, w których jedna z podstaw jest 3 razy dłuższa od drugiej oraz suma długości podstaw i wysokości trapezu jest równa 24 cm. a) Wyznacz długości boków trapezu, wiedząc, że jego pole jest równe 64cm² b) Wyznacz długości boków trapezu, który ma największe pole. Oblicz to pole.

Eta: Kto się "rzuca" na to zad.?

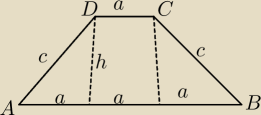
Mila: 3a+a+h=24 4a+h=24 a) P=64 cm²

	3a+a
P=		*h
	2

4a
	*h=64
2

2a*h=64/:2⇔a*h=32 4a+h=24 h=24−4a ======= a*(24−4a)=32 24a−4a²=32 ⇔ 4a²−24a+32=0 /:4 a²−6a+8=0 rozwiąż a>0 b)

	4a
P(a)=		*h
	2

P(a)=2a*h P(a)=2a*(24−4a)=48a−8a² parabola skierowana w dół, wartość największa dla x_w

	−48
aw =		=3
	2*(−8)

P(3)=48*3−8*9=72 dokończ , to już proste.

Eta: Mila czemu nie wyznaczyłaś od razu : 4a+h=24 ⇒ h= 24−4a dla a∊(0,6)

Mila: Czekałam na pytania Cersei.