Trygonometria Qmi: Trygonometria zadanie nierówności

	1
sin2 3x−√2 sin 3x +		= 0
	2

zał: t = sin3x

	1
t2−√2t+		= 0
	2

Δ = 0

	√2
to=
	2

	√2
sin 3x =
	2

dalej mam że

	√2
sin		= 45o
	2

ale dlaczego znikła to 3 co jest po sin. ?

wredulus:

	√2
raczej sin45o =
	2

Saizou :

	√2
sin3x=
	2

	π		3
3x=		+2kπ lub 3x=		π+2kπ
	4		4

Qmi: Nie wolno pisać tak jak ja napisałem? Dzięki Saizo, nie wiadziałem tylko co z tą 3 zrobić

Piotr 10: albo robisz sobie kolejne podstawienie, jesli sprawia Ci to problem 3x = p sin ( p ) =√2{2} .. itd

wredulus:

	√2
sin		≠ 45o <−−− co to jest 45o jaka to jest wartość liczbowa
	2

to tak jakbyś powiedział: Jadąc 50km/h w czasie 5km przejechałem drogę 6minut.

Saizou :

	√2		π
możesz ale wtedy arcsin(		)=
	2		4

funkcja odwrotna do sinusa, czy jakoś tak

Qmi: Oki. Tak szybciutko jeszcze tutaj. zał: cos x = t t = 0 cos x = 0

	π
x =		+ 2kπ <− może być zapisane miejsce zerowe w taki sposób, tak?
	2

Qmi: + kπ* , bo miejsce zerowe jest co kπ

Saizou : gdzie k∊C i będzie git xd

Qmi: Oki wredulus, po prostu wygodniej mi się tak liczy/czyta/piszę, ale wezmę to pod uwagę.

wredulus: teraz dobrze

Saizou : ale po co dajesz podstawienie do tak prostego przykładu to ja nie wiem ?

Qmi: Saizou, na przyszłość. Koleje zadanie

	x		√3
p{sin2		=
	2		2

	x		√3
|sin		| =
	2		2

	x		√3		√3
sin		=		v sin{x}{2} = −
	2		2		2

	√3		π
wiem że		to		ale dalej nie wiem co zrobić.
	2		3

Qmi:

	x		√3
√sin2		=
	2		2

(wszystko pod pierwiastkiem, tam w wiadomości wyżej nie wyszło mi. Od tego zaczynamy.

wredulus:

x		π		x		π
	=		+2kπ ⋁		= −		+2kπ
2		3		2		3

z tego wynika: x = ...... ⋁ x = ......

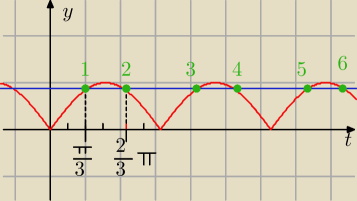
Saizou : to jest wykres lsintl (ten czerwony)

	√3
niebieski to prosta y=
	2

	x
naszym t=
	2

zapisujemy rozwiązania dla t

	π
t=		+kπ (powtarzalność co π, bo 1,3,5 to te same
	3

	2
t=		π+kπ (−ll−, bo 2,4,6 to te same )
	3

Qmi:

	2		2
x=		π+2kπ v x= −		π+2kπ
	3		3

i tyle? w zeszycie mam napisane:

	x		√3		x		√3
sin		=		v sin		= −
	2		2		2		2

x		π		x		4
	=		+2kπ v		=		+2kπ
2		3		2		3

x		π		x		5
	= π−		+ 2kπ v		=		+ 2kπ
2		3		2		3

	4π		10
x=		+4kπ v x=		π + 4kπ
	3		3

	4		10
x=		π+4kπ v x=		π+4kπ
	3		3

Czy to jest dobrze?

Qmi: Może ktoś policzyć to sposobem wredulus. Dzięki Saizou za odpowiedź.

Qmi: ~ podbijam

Saizou : ale sposób wredulusa jest dokładnie taki sam jak mój, tylko on wziął inne argumenty, bo sinus to funkcja okresowa

Qmi: W wiadomości 3 cze 2014 20:48 <− Napisałem wynik który mi wyszedł licząc ,,na piechotę" wredulusa i musiałem się gdzieś walnąć bo jest inny wynik

Saizou : nie walnąłeś się, bo ja mam obliczone t, a nie x zresztą Twoje rozwiązanie można zapisać za pomocą dwóch równań