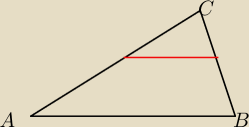
Twierdzenie Talesa Rafał: Witam proszę o cale rozwiązanie tego ćwiczenie, ponieważ nie rozumiem tego. Wykaż, że w dowolnym trójkącie odcinek łączący środki dwóch boków ma długość równą połowie długości trzeciego boku i jest do niego równoległy.

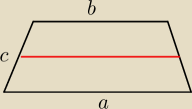
Rafał: I jeszcze trapez

Rafał: Podbijam. Bardzo proszę o pomoc

Saizou : podobieństwo trójkątów

c		2c
	=
x		y

	1
x=		y
	2

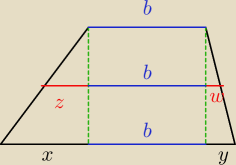
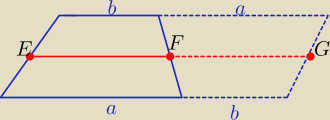
wredulus: odnośnie trójkąta −−− patrz tw. Talesa odnośnie trapezu ... patrz rysunek (a = x+b+y), a następnie tw. Talesa

Rafał: Tylko tyle wystarczy?

wredulus: Rafał −−− rusz głową ... rozwiąż do końca zadanie ... wyciągnij wnioski ... i je zapisz

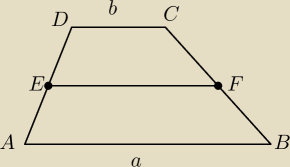
Saizou : można wektorowo EF=EA+AB+BF EF=ED+DC+CF =============+ 2EF=EA+AB+BF+ED+DC+CF wektory EA i ED są przeciwne tak samo CF i BF 2EF=AB+DC wracając do świata liczb 2lEFl=a+b

	a+b
lEFl=
	2

Rafał: pytanie miało być skierowane do Saizou Dalej sobie poradze. Dzięki panowie

Eta:

	1		a+b
|EG|= a+b to |EF|=		|EG|=
	2		2

PW: Opowiem dlaczego czerwona kreska jest równoległa do podstawy. Niech D będzie środkiem AC, zaś E − środkiem BC . Twierdzenie Talesa mówi, że jeśli ramiona kąta ACB przetniemy dwiema równoległymi − prostą AB i prostą przechodzącą przez D, to na ramionach kąta zostaną wyznaczone odcinki jednakowo proporcjonalne, w tym wypadku

	|CD|		|CX|
(1)		=		,
	|DA|		|XB|

gdzie X oznacza punkt, w którym posta przechodząca przez D przecina ramię CB. D jest środkiem odcinka CA, a więc lewa strona wzoru (1) jest równa 1, skąd

	|CX|
1 =
	|XB|

|CX| = |XB|, co oznacza, że X jest środkiem odcinka CB, czyli X = E. Wniosek: jeżeli prosta przechodzi przez D i jest równoległa do AB, to E należy do tej prostej. Zgodnie z odpowiednim aksjomatem przez punkty D i E przechodzi dokładnie jedna prosta, tak więc DE jest równoległa do AB.

Eta: Mnie by się nie chciało tyle pisać

Saizou : wolę wektory

Eta:

PW: Eta, ale nikt nie odpowiedział na pytanie − dlaczego jest równoległy? A odpowiedź jest tak łatwa, że aż trudna, dlatego napisałem