czworokat
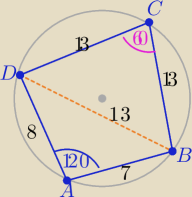
majster: Na czworokącie ABCD można opisać okrąg. Cięciwy AB i AD tego okręgu mają odpowiednio długość 7
i 8, zaś kąt BAD jest równy 120st. Wiedząc, że |DC| = |BC|, oblicz pole czworokąta ABCD.
3 cze 16:32
pigor: ..., np.
1) z tw. cosinusów: |BD|
2= 7
2+8
2−2*7*8cos(180
o−60
o)=
= 7
2+8
2+2*7*8cos60
o= 7
2+8
2+7*8 = 64+7*15= 169 ⇒
|BD|=13,
2) |∡BCD}=180
−120
o= 60
o z tw. o okręgu opisanym na czworokącie,
stąd i warunków zadania ΔBCD − równoboczny o boku 13, zatem
3) PABCD=P
ΔABD+P
ΔBCD=
12*7*8sin120
o+
14*13
2√3=
=
12*56sin60
o+
14*169
√3=
14*56
√3+
14*169
√3=
=
14(56+169)
√3=
14*225√3=
56,25√3 − szukane
pole.
3 cze 17:11
Eta:
3 cze 17:44
mietek: 
3 cze 17:46
Eta:
3 cze 17:52
pigor: ..., no i fajnie się...
uzupełnia−my
3 cze 17:54
Gorgo: Ale czemu najpierw jest − a potem + przy twierdzeniu Cosinusów ?
30 mar 16:57
dżins: w drugiej ćwiartce dla cos zmieniamy znak
24 sty 00:25
XD:
26 sty 18:28