Niech ktos pomoże Marlena424: Znałeść rozwiązanie optymalne następującego zagadnienia programowania liniowego: Maksimum funkcji f = 3x₁ +2x₂ przy warunkach ograniczających: x₁ +2x₂ ≤ 7 2x₁ +x₂ ≤ 8 x₂ ≤ 3 x₁ , x₂ ≥ 0.

Krzysiek: przy dwóch zmiennych najlepiej rozwiązać to zadanie geometrycznie.

Marlena424: Czyli jak sie za to wziąść ?

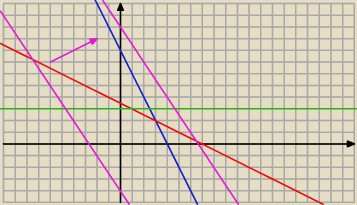
Krzysiek: fioletowe proste to funkcja f=3x+2y dla wybranych 'f' no i teraz zadanie polega na tym,że masz tak wybrać 'f' by maksymalnie tą prostą przesunąc (zgodnie ze strzałką−prostopadle do tej prostej) tak by ta prosta jeszcze przecinała obszar. no i dla tego punktu funkcja przyjmie największą wartość

Marlena424: tą fioletową musze przeciąć wszystkie te inne linie(funkcje) tak ? czyli że max wynosi 21 w punkcie (0,7)

Krzysiek: nie, wiesz jaki jest obszar który ograniczają te warunki? ja narysowałem tylko te funkcje

Marlena424: (1,3), (3,2), (0,0) (4,0) współne punkty to te tak ? Dobrze mysle,

Krzysiek: no i chyba jeszcze (0,3) to te punkty to wierzchołki obszaru. no i jak maksymalnie przesuniesz tą prostą by nadal stykała się z obszarem to punkt wspólny prostej i obszaru to (3,2) maksimum funkcji to f=9+4=13

Marlena424: Krzysiek ,jeśli tak moge do Ciebie mówić , powiedz mi jak narysowałeś tą główną funkcję f = 3x₁ +2x₂ bo inaczej mi wychodzi niż Tobie na rysunku

Marlena424: Niech ktoś pomoże ,pilne

Krzysiek: przecież napisałem,że te proste są dla pewnych 'f' a ty szukasz konkretnego 'f' takiego,żeby 'f' było największe i ta prosta przecinała obszar. Więc przyjmujesz sobie jakąkolwiek wartość za 'f' i rysujesz tą funkcję by potem ją przesunąć prostopadle do wektora [3,2]