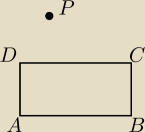
wykaż prawdziwość równania, dla dowolnego punktu P oddalonego od prostokąta Aga: AP² +PC² = DP²+ BP²

zawodus: Najprościej umieścić ten obiekt w układzie współrzędnych

Tymon: Przyjmijmy oznaczenie: <AB> = wektor AB; "◯" − iloczyn skalarny wektorów. Z równości przekątnych prostokąta mamy: (<AP>+<PC>)² = ((<DP>+<PB>)² (równość kwadratów skalarnych). Udowadniana równośc zajdzie zatem wtedy i tylko wtedy, gdy <AP>◯<PC> = <DP>◯<PB>. (*) Z relacji Chasle'a mamy <AP> = <AD> +<DP> i <PB>= <PC>+<CD> =<PC>−<AD> Kładąc powyższe do (*) otrzymujemy po redukcji <AD>◯<PC>=−<AD>◯<DP>, czyli <AD>◯(<PC> + <DP>) =0; ale <DP>+<PC> =<DC> równość (*) ( i w konsekwencji także równość będąca obiektem dowodu) przyjmuje przeto formę równowazną <AD>◯<DC>=0 , oczywistą ze względu na ortogonalność wektorów utworzonych przez sasiednie boki prostokąta. ♣

Tymon: Pomyłka w maszynopisaniu: "Z relacji Chasle'a mamy <AP> = <AD> +<DP> i <PB>= <PC>+<CB> =<PC>−<AD>"