planimetria pomocy pietrusd: Na trójkącie równoramiennym ostrokątnym opisano okrąg o r=13. Wysokość trójkata ma 18 cm. Oblicz ramię.

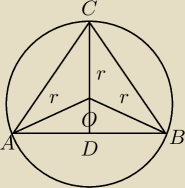
kyrtap: h = IADI = 18 r = IAOI = IBOI = ICOI = 13 1) Z tw . Pitagorasa dla Δ ODB znając dł. boków IDOI = 18 − 13 i IOBI = 13 oblicz dł boku IDBI 2) Potem zauważ że ΔCDB ∼ ΔODB (cecha kkk). Stąd wyliczysz ramię, mając zależność:

	ICDI
		= {ICBI}{IBOI}
	IDBI

kyrtap: Poprawiam

ICDI		ICBI
	=
IDBI		IBOI

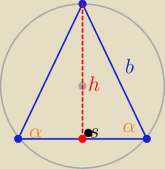Eta: Trójkąt ostrokątny α∊(0^o,90^o) i b>0

	h
sinα=
	b

	b		b
z tw. sinusów		=2R ⇒ sinα=
	sinα		2R

h		b
	=		⇒ b2=2R*h ⇒ b=...........
b		2R