Funkcja Logarytmiczna katB: Narysuj wykres funkcji i omów jej własności : f_(x) = |log_1/3 |x+2| | Jak się do tego zabrać ? I : y = log_1/3 II : i tutaj rozpisać wartość bezwzględną ? x+2 ≥ 0 Nie rozumiem , przesunąć o wektor w którym momencie co tutaj mam zrobić ? III : odbicie końcowe względem osi OX Prosiłbym o pomoc w II.

daras: wolfram.cośtam wklep

zawodus: Bzdury co to jest log_1/3?

kochanus_niepospolitus: 1) y=log_1/3 x szkic 2) y=log_1/3 (x+2) szkic (czyli przesuwasz w którą stronę i o ile?) 3) y=log_1/3 |x+2| szkic (wszystko co było na prawo od OY 'odbijasz symetrycznie' także na lewo od OY 4) y = |log_1/3 |x+2| | szkic (wszystko co było poniżej osi OX 'przeskakuje' do góry) koooniec

katB:

1
	to podstawa logarytmu.
3

log_ab = c <=> a^c = b

katB: kochanus , dzięki 2) Wiem , przesuwam w lewo o 2 3) DZIĘKI WIELKIE ! ( zapomniałem jakoś ) 4) wiem wiem Dzięki jeszcze raz

katB: zwodus pomyliłem się , ale wiesz o co mi chodziło : y = log_1/3x

katB: sry *zawodus

zawodus: Niestety, ale jest źle

katB: no to co jest nie tak, wyjaśnij nam , bo nie wiem o co Ci chodzi.

Lukas: sry ? co to znaczy ?

katB: A nie przypadkiem najpierw odbić względem osi OY a potem przesunąć ?

zawodus: Nasz kochania zrobił błąd myślę, że poczekamy i poozwolimy mu się poprawić

katB: Lukas : sry = sorry = przepraszam

kochanus_niepospolitus: Lukas ... sry ... dwie opcje: 1) sorry 2) syry (zabierz ze stołu) ... mi osobiście bardziej pasuje druga opcja

zawodus: Tak najpierw f(|x|), a potem przesunięcie

Lukas: Tyle się uczy angielskiego i jakieś farmazony pisze sry co to jest ? sorry się pisze..

kochanus_niepospolitus: zawodus ... bluźnisz a szczerze ... błędu nie widzę zwykły log −> przeusnięcie −> I i IV ćwiartka kopiowane na II i III −> III i IV ćwiartka wycięte i wklejone w II i I ćwiartkę ... jak dla mnie wygląda ok

katB: Przepraszam że zaburzyłem twój światopogląd i wywołałem w tobie frustracje. Po drugie skąd ty możesz wiedzieć ile ja się uczę angielskiego ^^

zawodus: Kochanus nie pogrążaj się Kolejność ma kolosalne znaczenie tutaj

Lukas: Własnie widzę, że chyba nie tylko z matematyką problem skoro proste słówko po angielsku to problem...

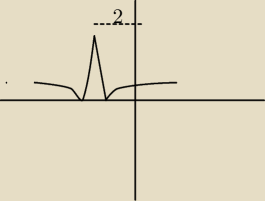
katB: Takie coś mi wyszło

katB: Lukas , nie jest problemem , ale widzę, że potrafisz czepiać się wszystkiego, dobrze będę normalnie pisał. Przestań zachowywać się jak jakiś sztywniak i czepiać się innych ludzi o byle gówno. Nie chcesz mi pomóc to nie pisz tutaj w tym temacie nic, na razie to mi zawracasz głowę swoimi poglądami o błędach w pisowni słówek z angielskiego.

zawodus: KatB

zawodus: To teraz ćwiczenie na zapamiętanie zamień kolejność kroku 2 i 3 i zobacz co otrzymasz Sprobuj wskazać wzór otrzymanej funkcji

katB: I : y = log_1/3x II : y = log_1/3|x| − odbicie funkcji względem osi OY i pozostawienie funkcji z prawej III : y = log_1/3|x+2| − przesunięcie o 2 jednostki w lewo IV : y = | log_1/3|x+2| | − odbicie względem osi OX wszystkiego co ma wartość y < 0 Własności : D = R ZW = (0;+nk) f malejąca dla x ∊ (−nk,3)∪(−2,−1) f rosnąca dla x ∊ (−3;2)u(−1;+nk) nie ma wart. najw,najm as pionowa x = −2 funkcja różnowartościowa f > 0 dla x ∊ R\{−3;−1} f < 0 ni ma coś jeszcze i dobrze ?

zawodus: Własności nie bardzo Źle jest dziedzina, zbiór wartości, przedziały monotoniczności, ma wartość najmniejszą, nie jest różni wartościowa. Ogólnie nie wiem co wymaga jeszcze twój nauczyciel. Może miejsca zerowe? Przyjrzyj się jeszcze raz wykresowi, bo te własności jak widzisz są fatalnie zrobione

katB: pytanie ZW = <0;+nk) ? czy ZW = (0;+nk) bo od tego zależy czy będzie najmniejsza wartość funkcji Ale chyba <0;+nk) czyli najmniejsza wart. funkcji y = 0

zawodus: To Rozwiąż równanie f(x)=0 i się przekonasz

katB: D : x+2 > 0 1/3 ≠ 1 ZW = <0;+nk) wartość najmniejsza y = 0 MZ : x = −3 x = −1 Funkcja rośnie <−1;+nk) u <−3;−2) Funkcja maleje (−nk;−3> u (−2;−1>

kyrtap: Własności funkcji: 1. Dziedzina 2 . Zbiór wartości 3. Miejsca zerowe 4. Monotoniczność funkcji 5. f(x) >0 ⇔x∊..... f(x) <0 ⇔ x∊ 6. Parzystość, nieparzystość funkcji 7. Różnowartościowość 8. Najmniejsza i największa wartość funkcji 9. Asymptoty jeżeli ma funkcja

zawodus: Dziedzina źle i źle przedziały Problem nie polegał z przedziałami na ich wyborze, tylko na zapisie odpowiedzi

katB: D : x > −2 ZW = ( 0 ; +nk) Pogubiłem się kiedy otwarte a kiedy zamknięte nawiasy.

katB: D : x = R \ {0} soory zapomniałem , wartość bezwzględna.

katB: D : x = R \ {−2} sorry jeszcze raz.

zawodus: Dziedzina cały czas źle ! Co jest argumentem funkcji?

zawodus: Teraz Co z tym zbiorem? Jest to 0 czy nie?

katB: Jest.

zawodus: To trzeba domykać Co z przedziałami monotoniczności?

katB: 1. D = R\{−2} 2. ZW = <0;+nk) 3. MZ : x = −3 ; x = −1 4. funkcja_maleje dla x ∊ (−nk;−3> u (−2;−1> funkcja_rośnie dla x ∊ <−3;−2) u <−1;+nk) 5. f > 0 dla x ∊ R \ {−3,−1} 6. funkcja parzysta 7. najmniejsza wartość funkcji y = 0 dla x = −3 ; x = −1 8. Asymptota pionowa x = −2

zawodus: 5. Wyrzuć jeszcze −2 6. To nie prawda. 4 usuń te znaki sumy i napisz ',' , bo nauczyciel cie oskalpuje Teraz mogłoby być

katB: Dzięki !

zawodus:

AL: zmie.ń kategorię na C albo D