Stereometria
Marcin: w ostrosłupie prawidłowym czworokątnym ściany boczne są trójkątami równobocznymi o boku
długości 4. Oblicz kąt, jakie tworzą dwie ściany tego ostrosłupa
Pomocy

Moglibyście rozwiązać mi to? Lepiej łapie jak sam sobie roztłumaczę skąd to wszystko
się wzięło, dzięki
1 cze 21:29
Lukas:
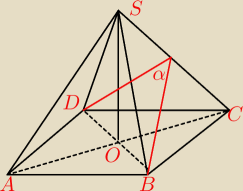
a−długość boku trójkąta
h=2
√3
DB−przekątna kwadratu
d=a
√2
d=4
√2
Z twierdzenia cosinusów
(4
√2)
2=(2
√3)
2+(2
√3)
2−2*2
√3*2
√3*cosα
32=12+12−24cosα
8=−24cosα
1 cze 21:35
Mila:
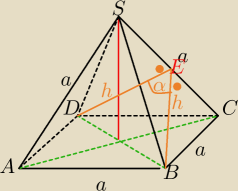
a=4
|DB|=a
√2=4
√2
Z tw. cosinusów w ΔBED:
(4
√2)
2=(2
√3)
2+(2
√3)
2−2*2
√3*2
√3 cosα
8=−24 cosα
odczytajesz w tablicach
cosx≈0,3333
x ≈70,5
o
α=180
o−70,5
o=109,5
o
1 cze 21:48
Marcin: Dziękuję
1 cze 21:58
Bogdan:
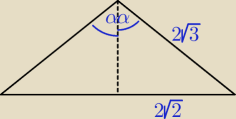
| | √2 | |
i bez twierdzenia cosinusów: sinα = |
| |
| | √3 | |
α = 0,9553166 [rad] ⇒ 2α = 1,9106332 [rad] = 109,47122
o
1 cze 22:11
 Moglibyście rozwiązać mi to? Lepiej łapie jak sam sobie roztłumaczę skąd to wszystko
się wzięło, dzięki
Moglibyście rozwiązać mi to? Lepiej łapie jak sam sobie roztłumaczę skąd to wszystko
się wzięło, dzięki

 a=4
a=4
