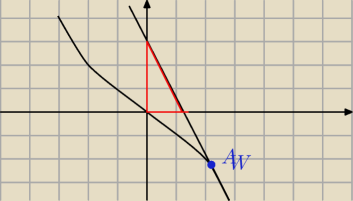
Zadanie Znajdz punkt olkaq: W którym punkcie należy poprowadzić styczną do wykresu f(x) = −x³, aby pole trójkąta ograniczonego styczną i osiami układu współrzędnych wynosiło 54. Według mnie równanie tej stycznej będzie tak wyglądało: y + x_o³ = −3x₀²( x − x_o) y = 3x_o³*x + 2x_o²

olkaq:

pigor: ..., no nie, bo źle przekształciłeś, otóż f '(x_o)=−3x²_o, wtedy y+ x³_o= −3x²_o(x − xo) ⇔ y = −3x_o²x+2x³_o − równanie stycznej w punkcie P=(x_o,y_o)= (x_o,−x³_o)=? i x_o≠0 do danej krzywej y= −x³, no to ta prosta styczna przecina oś OX w punkcie (a,0) takim, że −3x²_oa+2x³_o=0 ⇔ ⇔ 3a=2x_o ⇔ a=²₃x_o, oraz oś OY w punkcie (0,b) takim, że b=2x_o, zatem z warunku zadania P_Δ=54 ⇔ ¹₂ab=54 ⇔ ab=108 ⇔ ⇔ ²₃x_o*2x_o= 108 ⇔ 4x²_o= 108*3 /:4 ⇔ x²_o=27*3 ⇔ |x_o|=9 ⇔ ⇔ x_o= ±9 ⇒ (x_o,y_o)= (−9,−9³) v (x_o,y_o)= (9,9³) ; odp. P=(−9,−729), lub P=(9,729) − szukane punkty styczności . ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− p.s. rozwiązanie można znaleźć także bez znajomości pojęcia pochodnej funkcji .