Rozwiąż równanie mordini pck: cos(^2π_x)+¹₂x²=2x−3

razor:

	1
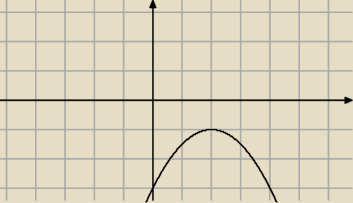
y = −		x2 + 2x − 3
	2

cosα przyjmuje wartości z przedziału <−1,1>, z wykresu widać że jedynym miejscem, w którym te

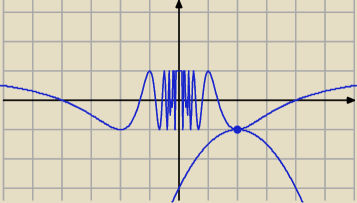
	2π
funkcje mogą się spotkać jest x = 2, wtedy cos		musi się równać −1. Sprawdźmy:
	x

	2π
cos		= cosπ = −1
	2

Zatem rozwiązaniem tego równania jest x = 2

Bogdan:

	1
y = −		x2 + 2x − 3, to parabola z wierzchołkiem W = (2, −1)
	2

	1		2π
To jest jedyny możliwy punkt wspólny linii: y = −		x2 + 2x − 3 i linii y = cos(		)
	2		x

	1
Sprawdzenie: −		*22 + 2*2 − 3 = −1, więc rozwiązaniem podanego równania jest x = 2
	2