Ciąg (b_n) określony jest wzorem b_n = (n-7)(n + 8). Liczba ujemnych wyrazów cią
vvaste: Ciąg (bn) określony jest wzorem bn = (n−7)(n + 8). Liczba ujemnych wyrazów ciągu (bn) jest
równa...?
Najmniejszy wyraz ciągu (an) o wyrazie ogólnym an = (n−6)2 3 jest równy...?
Jak należy się zabrać za te zadania?
1 cze 17:53
Lukas:
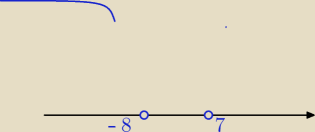
(n−7)(n+8)<0
n∊N
Liczba wyrazów mniejszych od zera to 7
a
n=(n−6)
2 ? 3 przepisz dobrze najpierw
1 cze 17:57
Janek191:
b
n = ( n − 7)*( n + 8) < 0 n
1 = − 8 n
2 = 7
więc
n ∊ ( − 8 ; 7 ) ∩ N
+ = { 1 ,2, 3, 4, 5,6 }
Odp. 6
( a
1, a
2, a
3, a
4, a
5, a
6 )
oraz rysunek
1 cze 17:58
vvaste: an = (n−6)2 + 3, przepraszam.
1 cze 18:05
Lukas:
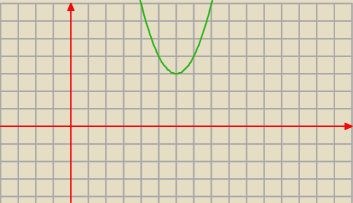
a
6=3 z własności f.kwadratowej
1 cze 18:06
vvaste: To w końcu 7 wyrazów ujemnych czy 6? Ja zaznaczyłam, że 7, a odpowiedź jednak była zła...
1 cze 18:12
Janek191:
6 !
Nie ma wyrazu a
0 !
1 cze 18:18
vvaste: No właśnie.
Dziękuje.
1 cze 18:19