Zadania olkaq: Wykaż, że pole trójkąta ograniczonego styczną do hiperboli xy=k² (k różne od 0), w punkcie P należącym do xy=k² oraz asymptoty tej funkcji nie zależy od współrzędnych punktu.

Mila:

	k2
m: y=f(x)=
	x

	k2
P=(a,		)∊m
	a

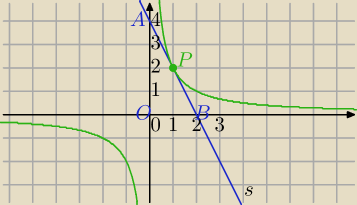
Styczna y=f'(a)x +b

	−k2
f'(x)=
	x2

	−k2
f'(a)=
	a2

	−k2
s: y=		*x+b i P∊s
	a2

k2		−k2		2k2
	=		*a+b⇔b=
a		a2		a

	−k2		2k2
s: y=		*x+
	a2		a

	1
PΔAOB=		*|OA|*OB|
	2

	2k2
|OA|=|b|=
	a

	−k2		2k2		−k2		2k2
B: miejsce zerowe y=		*x+		⇔		*x+		=0
	a2		a		a2		a

−k2		2k2
	*x=−		⇔
a2		a

	2k2		a2
x=−		*		=2a
	a		−k2

	1		1		2k2
PΔAOB=		*|OA|*OB|=		*|		|*|2a|=2k2
	2		2		a

cnw

lipa: Widzę, że wrzucasz zadanka i czekasz na gotowca, albo wcale Cię nie interesuje, że ktoś Ci rozwiązał.

lolek: a tyle się dziewczyna naliczyła...

pigor: .., lub bez pochodnej dowolny punkt (x,y)= (x, ¹_xk²) hiperboli xy=k² będzie punktem styczności prostej w postaci kierunkowej ^x_a+^y_b=1 i ab≠0 z wykresem danej hiperboli jeśli równanie ^x_a + ^k2_xb=1 /abk² ⇔ bx²+ak²=abx ⇔ ⇔ bx²−abx+ak²=0 kwadratowe ma dokładnie 1 rozwiązanie, czyli ⇔ Δ=0 ⇔ a²b²−4abk²=0 ⇔ ab(ab−4k²)=0 ⇔ ab−4k²=0 ⇔ ab=4k², a wtedy istotnie, pole Δ o którym mowa w zadaniu wyrażone wzorem P_Δ=¹₂ab= ¹₂*4k²= 2k² jest niezależne od współrzędnych x,y dowolnego danej hiperboli, co tez należało wykazać . ...