katy zewnetrzne
shadow: W prostokącie, który nie jest kwadratem, poprowadzono dwusieczne kątów zewnętrznych. Udowodnij,
że punkty przecięcia tych dwusiecznych są wierzchołkami kwadratu.
1 cze 14:54
Seyin:
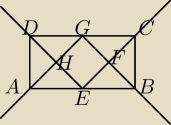
Teza: EFGH− kwadrat
Dowod:
KGAE=KGAD =90/2 − analogicznie przy pozostalych bokach − dwusieczne kata 90
KAHE=90 − z sumy miar katow w trojkacie AHE
KEHG = 90 − wierzcholkowe
Analogicznie dla pozostalych
KCBG=KBGC Trojkat GCB rownoramienny
Ponadto KBEF=KEBF − Trojkat EBF rownoramienny
Ponadto zauwazam, ze trojkat EBF przystajacy do trojkata GCF z cechy kbk
Otrzymalem ze GF=FE Analogicznie GH=HE
Co konczy dowod
1 cze 15:23
mix:
1 cze 15:28
mix:

1 cze 15:28
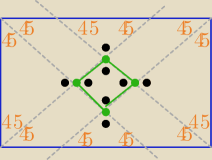
Seyin: Z tym ze same miary katow prowadza do tezy − jest to prostokat

1 cze 15:31
mix:
Odległości między prostymi równoległymi ( dwusiecznymi) są równe
wniosek: .........
1 cze 15:35
shadow: a jakby to zrobić dla dwusiecznych kątów wewnętrznych?
1 cze 15:40
mix:
Właśnie podałam Ci dowód dla dwusiecznych kątów wewnętrznych (rys. 1 cze 15:28
1 cze 15:47
shadow: u góry pytałam dla zewnętrznych, dla wewnętrznych miałam tak jak ty mix i teraz zwątpiłam w
poprawność, potrzebuję jeszcze dla zewnętrznych
1 cze 15:49
mix:
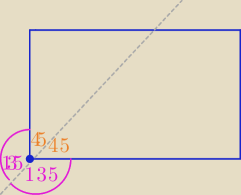
1 cze 16:09
shadow: czyli dowod taki sam?
1 cze 18:09
 Teza: EFGH− kwadrat
Dowod:
KGAE=KGAD =90/2 − analogicznie przy pozostalych bokach − dwusieczne kata 90
KAHE=90 − z sumy miar katow w trojkacie AHE
KEHG = 90 − wierzcholkowe
Analogicznie dla pozostalych
KCBG=KBGC Trojkat GCB rownoramienny
Ponadto KBEF=KEBF − Trojkat EBF rownoramienny
Ponadto zauwazam, ze trojkat EBF przystajacy do trojkata GCF z cechy kbk
Otrzymalem ze GF=FE Analogicznie GH=HE
Co konczy dowod
Teza: EFGH− kwadrat
Dowod:
KGAE=KGAD =90/2 − analogicznie przy pozostalych bokach − dwusieczne kata 90
KAHE=90 − z sumy miar katow w trojkacie AHE
KEHG = 90 − wierzcholkowe
Analogicznie dla pozostalych
KCBG=KBGC Trojkat GCB rownoramienny
Ponadto KBEF=KEBF − Trojkat EBF rownoramienny
Ponadto zauwazam, ze trojkat EBF przystajacy do trojkata GCF z cechy kbk
Otrzymalem ze GF=FE Analogicznie GH=HE
Co konczy dowod



