Dowód - rysunek i wskazówka
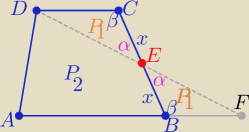
Maron: Dany jest czworokąt ABCF, na którym AB || CD. Na boku BC wybrano taki punkt E, że |EC| = |CD| i
|EB| = |BA|. Wykaż, że kąt AED jest prosty.
Poszę o rysunek i jakąś wskazówkę o ile to możliwe

1 cze 13:09
Saizou :
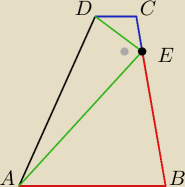
1 cze 13:16
nissan 2.0.TD: Uwierz mi. I.A. Maron nie mialby takich kolpotow

1 cze 13:19
Maron: A jakaś wskazówka ? Nie mam pojęcia jak powinienem zacząć

1 cze 13:20
mix:
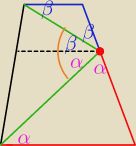
1 cze 13:25
Maron: Wszystko ok, tylko nie wiem skąd Ci się wzięło tam przy wysokości od punktu E na gorze β a na
dole kąta α. Mógłybś pomóc ?
1 cze 13:26
Saizou :
∡DCE=180−2β
∡ABC=180−2α
suma miar kątów przy jednym ramieniu trapezu wynosi 180
180−2α+180−2β=180
2α+2β=180
α+β=90
∠AED+α+β=180 jako kąt półpełny
∠AED=90
1 cze 13:37
mix:

1 cze 13:37
Saizou :
mix a gdzie

od
Ety 
1 cze 13:38
mix:


1 cze 13:40
Saizou : 
na szarlotkę będzie xd
1 cze 13:42
Maron: Dzięki, teraz wszystko rozumiem. Ale zostało mi jeszcze kilka zadanek i pewnie z nimi również
będę potrzebował mniejszej lub większej pomocy, więc będę pisał w tym temacie

1 cze 13:47
Maron:
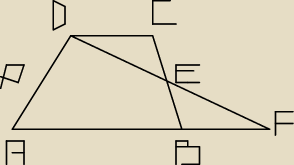
No właśnie ...
Punkt E jest środkiem odcinka BC. Uzasadnij, że pole trapezu
ABCD i pole trójkąta
AFD są równe.
Jeśli bym podzielił to tak ,że górna podstawa to X dolna Y to mógłbym zrobić ,że
X+Y2 =
odległość od E do punktu P, ale nie wiem co dalej i czy w ogóle to się przyda ?
1 cze 13:53
Saizou : istotą jest pokazanie że BF=CD
PS.
podobieństwo trójkątów, a nawet przystawanie

1 cze 13:55
Saizou :
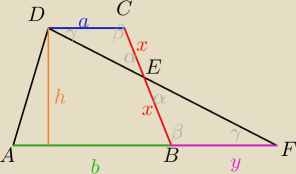
ΔBEF~ΔCDE ⇒ a=y
i już praktycznie koniec xd
1 cze 14:00
mix:
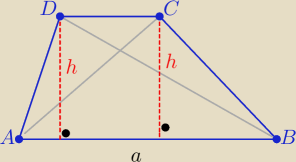
Trójkąty BEF i DCE są przystające z cechy (kbk)
zatem mają równe pola
P1
to : ....... dokończ uzasadnienie
1 cze 14:05
mix:

1 cze 14:07
Maron: Wyszło mi, że PABCD = 12 (a+b) * h
PΔADF= 12 (b+y) *h
I jak mam udowodnić, że pola są równe ?
1 cze 16:01
mix:
P(AFD)=P2+P1 , P(ABCD)= P2+P1 ⇒ ...........
1 cze 16:06
Maron: Dobra, mam. a=b, bo są przystające

.
Jeszcze :
Trójkąt o bokach 10,24,26 wpisano w okrąg. Wykaż, że pole koła ograniczonego tym okręgiem jest
równe 169π.
1 cze 16:06
pigor: ... , np. tak : zauważ , że dany trójkąt jest ...

prostokątny,
bo 10
2+24
2= 26
2, wtedy R=13 , no to
Pk= πR
2= 13
2π=
169π , c.n.w.
1 cze 16:34
Maron: Jeszcze jedno :
Dany jest trapez ABCD, w którym AB || CD. Wykaż, że pola trójkątów ABC i ABD są równe.
1 cze 17:55
Eta:
| | a*h | | a*h | |
P(ABC)= |
| , P(ABD)= |
| ⇒ wniosek .... |
| | 2 | | 2 | |
1 cze 18:06
Maron: No i jeszcze jedno

:
W trójkącie ABC na boku AB zaznaczono punkty D i E tak, że |AD| = |EB| =
15 |AB|. Wykaż,
że P
DEC = u {3}{2} (P
ADC + P
EBC).
1 cze 18:20
Saizou :
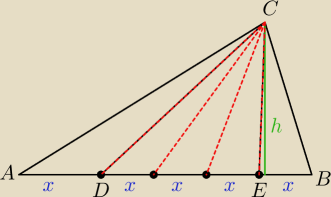
zauważmy że każdy z tych małych trójkątów ma jednakowe pole
i już po kłopocie

1 cze 19:12
Maron: A skąd wiemy, że każdy ma takie samo pole ?
1 cze 21:34
Maron: Dobra wiem już

1 cze 21:41






 od Ety
od Ety 


 na szarlotkę będzie xd
na szarlotkę będzie xd

 No właśnie ...
Punkt E jest środkiem odcinka BC. Uzasadnij, że pole trapezuABCD i pole trójkątaAFD są równe.
Jeśli bym podzielił to tak ,że górna podstawa to X dolna Y to mógłbym zrobić ,że X+Y2 =
odległość od E do punktu P, ale nie wiem co dalej i czy w ogóle to się przyda ?
No właśnie ...
Punkt E jest środkiem odcinka BC. Uzasadnij, że pole trapezuABCD i pole trójkątaAFD są równe.
Jeśli bym podzielił to tak ,że górna podstawa to X dolna Y to mógłbym zrobić ,że X+Y2 =
odległość od E do punktu P, ale nie wiem co dalej i czy w ogóle to się przyda ?


 Trójkąty BEF i DCE są przystające z cechy (kbk)
zatem mają równe pola P1
to : ....... dokończ uzasadnienie
Trójkąty BEF i DCE są przystające z cechy (kbk)
zatem mają równe pola P1
to : ....... dokończ uzasadnienie

 .
Jeszcze :
Trójkąt o bokach 10,24,26 wpisano w okrąg. Wykaż, że pole koła ograniczonego tym okręgiem jest
równe 169π.
.
Jeszcze :
Trójkąt o bokach 10,24,26 wpisano w okrąg. Wykaż, że pole koła ograniczonego tym okręgiem jest
równe 169π.
 prostokątny,
bo 102+242= 262, wtedy R=13 , no to Pk= πR2= 132π= 169π , c.n.w.
prostokątny,
bo 102+242= 262, wtedy R=13 , no to Pk= πR2= 132π= 169π , c.n.w.

 :
W trójkącie ABC na boku AB zaznaczono punkty D i E tak, że |AD| = |EB| = 15 |AB|. Wykaż,
że PDEC = u {3}{2} (PADC + PEBC).
:
W trójkącie ABC na boku AB zaznaczono punkty D i E tak, że |AD| = |EB| = 15 |AB|. Wykaż,
że PDEC = u {3}{2} (PADC + PEBC).
 zauważmy że każdy z tych małych trójkątów ma jednakowe pole
i już po kłopocie
zauważmy że każdy z tych małych trójkątów ma jednakowe pole
i już po kłopocie 
