ekstrema Alois~: ekstrema lokalne funkcji: 1) f(x,y) = (cosx + cosy)² + (sinx+siny)² cosxsiny − sinxcosy=0 sinxcosy − cosxsiny=0 nie mam pojecia jak rozwiazac ten uklad 2)f(x,y) = x √y+1 + y √x+1

	y
√y+1 +		= 0
	2√x+1

	x
√x+1 +		= 0
	2√y+1

i sie zacielam na ukladzie ale zaraz go dalej bede meczyc moze wyjdzie bardzo bedzie mi milo jesli dostane odpowiedz do niego i bede mogla sprawdzic

Trivial: Zadanie 1: f(x,y) = cos²x + cos²y + 2cosxcosy + sin²x + sin²y + 2sinxsiny = 2 + 2(cosxcosy + sinxsiny) = 2 + 2cos(x−y). Minimum (równe 0), gdy cos(x−y) = −1. Maximum (równe 4), gdy cos(x−y) = 1.

Alois~: ale czy to jest do wyliczenia przez pochodne czastkowe

Alois~: chyba juz mam !

Trivial: A nie wiem. Dlaczego liczyć coś takiego przez pochodne cząstkowe? Przecież to jest dużo bardziej czasochłonne.

Alois~: tylko mi wychodzi jakas głupota chyba uklad: sin(y−x)= 0 sin(x−y) = 0

Alois~: bo mam takie polecenie kolokwium obejmuje pochodne czastkowe dziękuje za odpowiedzi moze sie dolicze wreszcie chociaz 2 raz to samo wyszlo

Trivial: A czemu głupota? Każda liczba spełniająca cos(u) = ±1 spełnia także sin(u) = 0. Moim sposobem od razu wiesz czy jest to minimum czy maksimum.

Alois~: a to nie bedzie ze y−x = 0 x−y= 0 y=x ? czyli ze wszystkie spelniaja ? to jak mam okreslic z tego skoro konkretnego punktu nie dostaje

Trivial: x−y = kπ (oba równania).

Alois~: zgłupiałam bo nie wiem jak to powyliczac , w sensie jakie punkty potem do wyznacznika wstawic

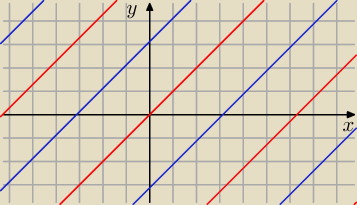
Trivial: Mówiłem, że to czasochłonne. Rozwiązaniami nie są pojedyncze punkty ale rodziny prostych (rysunek, czerwone − maksimum, niebieskie − minimum). Spełniają one równanie: x−y = kπ Tutaj wykres tej funkcji: http://www.wolframalpha.com/input/?i=2+%2B+2*cos%28x-y%29 Hesjan jest następujący:

	−2cos(x−y) 2cos(x−y) 2cos(x−y) −2cos(x−y)		−1 1 1 −1
H =		= 2cos(x−y)

	−1 1 1 −1		−1 1 1 −1
= 2cos(kπ)		= 2(−1)k

Teraz dwa przypadki, k parzyste, k nieparzyste i masz swoje rozwiązanie.

Alois~: dziękuje bardzo !