linearyzacja równania różniczkowego Kamil:

d2y		dy
	+5		+3y=sin(y)
dt2		dt

dokonać linearyzacja równania dla małych odchyłek, zakładając, że : a) x=0 b) x=π Zaznaczam, że nie miałem styczności prędzej z linearyzacją i chciałbym się nauczyć i potrzebowałbym przykładów jak rozwiązać, może też nie do końca rozumiem co ma oznaczać zwrot "dla małych odchyłek"

Kamil: help

Trivial: Chodzi o przybliżenie sin(y) ≈ y dla dostatecznie małego y.

Trivial: Tylko że to chyba powinno być sin(x), a nie sin(y).

Trivial: W ogóle masz jakiś chaos: tu x, tam t. Przepisz to równanie porządnie.

Kamil: znaczy tak przykład jest przepisany dobrze tylko podpunkty źle Poprawka a) y=0 b) y=π

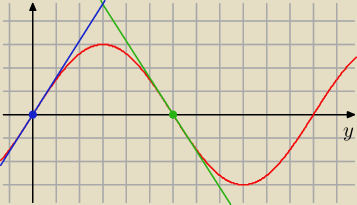
Trivial: a) sin(y) ≈ y b) sin(y) = −sin(y−π) ≈ π−y. Zobacz na wykresie porównanie wartości przybliżonych z dokładnymi dla różnych wartości y.