zadanka zawodus: Mila jeśli możesz to zajrzyj Mam pytanko. Czy uważasz, że polecenie zadania za poprawne? Wyznacz równanie hiperboli przechodzącej przez punkt A=(−2,−1), której osiami symetrii są proste y=x+4, y=2−x

Godzio: Może Milą nie jestem, ale gdzie widzisz jakiś błąd? (mówię tu o poleceniu, bo nie rozwiązywałem tego, w którym może się trafić jakaś sprzeczność)

zawodus: Chodzi mi o to, że nie każda hiperbola jest funkcją homograficzną (zadanie z tego działu). Da się to rozwiązać nie zakładając, że mówimy o funkcji homograficznej?

Godzio: Pewnie masz rację, ale gdyby tak myśleć to w ogóle nie powinniśmy rozpatrywać funkcji homograficznej tylko prawdziwą hiperbolę tzn.

x2		y2
	−		= 1 (ewentualnie z jakimś przesunięciem).
a2		b2

Rozumiem, że Twoje pytanie jest odnośnie innych funkcji, nie koniecznie homograficznych? Czy to zadanie jest z jakiegoś zbioru, który ma na początku każdego działu informacje w pigułce? Może tam było definiowane co to jest dokładnie hiperbola?

zawodus: To jest podręcznik do LO, zatem takiej informacji tam nie ma na pewno

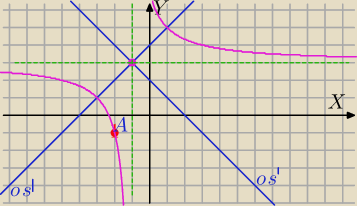
Mila: Rozważam hiperbolę równoosiową o równaniu:

	a
(1) y=
	x

(0,0) środek symetrii hiperboli y=x i y=−x osie symetrii hiperboli równoosiowej (1)

	a
S=(−1,3) środek symetrii hiperboli po translacji y=		o wektor [−1,3]
	x

	a
y=		+3
	x+1

	a
−1=		+3
	−2+1

a=4

	4
y=		+3
	x+1

==========

nissan 2.0.TD: Dlaczego uwaza Pani ze to bedzie hiperbola rownoosiawa a nie roznoosiawa ? Moge prosic o wyjasnienie ?

zawodus: Dzięki Mila Zastanawia mnie tylko fakt, dlaczego przyjęłaś takie założenie

mix:

	a
Osie symetrii hiperboli y=		: y= x i y= −x
	x

osie symetrii po translacji o wektor [−1,3] y−3=x+1 i y−3= −(x+1) y=x+4 i y=−x+2 −−−− takie osie symetrii masz w treści zadania

	a
zatem f(x)=		+3 i A(−2,−1) ⇒ a=4
	x+1

	4
f(x)=		+3
	x+1

Mlodziak: Mila to w ogole rzeznik z majcy

Mila: Zawodus, napisałeś, zadanie z LO.

zawodus: Tylko, myślę że powinna być wzmianka o jaką hiperbolę chodzi Bardziej się raczej domyślamy