objetosc swobodny: Obliczyć objętośc bryły ograniczonej powierzchniami y²−2+1=0, x−y=3, z=2x+y, z=0

Xawi: Tedy szmedy aby nie koło komendy. Kiedyś to byli czasy a ty sie jakimis bryłami martwisz

Krzysiek: coś błędnie przepisałeś pierwsze równanie krzywej. granice całkowania dla 'z' masz dane wystarczy narysować pierwszą i drugą krzywą i określić granice całkowania.

swobodny: miało być y²−x+1=0 CZyli, że za z mam podstawić i wyjdzie 0=2x+y ? W ogóle co to jest za bryła? bo ja tutaj widze że mam odwróconą parabolę, jakąś prostą i tyle.

Xawi: oj ciezka sprawa z toba

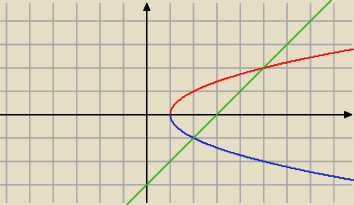
Krzysiek: napisałem narysuj pierwszą i drugą krzywą ale już na płaszczyźnie to rysujesz. z następnymi równaniami nic nie robisz. one określają granice całkowania dla zmiennej 'z' z∊[0,2x+y] .

ZDR: swobodny i tak nie zdasz

swobodny: Krzysiek: chyba mam −1<y<2 1<x<y+3 w takim razie będzie: ∫∫_D(2x+y)dxdy=∫₋₁² ∫₁ ^y+3(2x+y)dxdy

swobodny: ta dolna granica mnie zastanawia, albo tam będzie 1 albo √x. Tyle tylko że będzie potem problem zrobić √−1... Prosze o odpowiedź

Krzysiek: y²+1≤x≤3−y

swobodny: nie no chyba raczej 3+y x−y=3 x=y+3

Krzysiek: oczywiście,że tak.

swobodny: Dzięki, bardzo mi pomogłeś!