czworoscian

czworoscian Katti:

	16√2
Oblicz wysokość ściany bocznej czworościanu foremnego którego objętość wynosi
	3

30 maj 13:03

jerey: wiesz co to czworościan foremny?

30 maj 13:08

Katti: tak, to jest wielościan zbudowany z 4 trójkątów równobocznych

30 maj 13:09

Katti:

1		16√2
	Pp * H =
3		3

30 maj 13:10

jerey: z czym masz problem?

30 maj 13:10

Katti: Najpierw sam źle rysujesz rysunek a teraz się mądrzysz. Nie chcesz to nie pomagaj i tyle, pozdrawiam emotka

30 maj 13:11

jerey: chcę Ci pomóc, chcę sie dowiedziec z czym masz problem?

30 maj 13:12

Katti:

1		a² √3		16 √2
	*		* H =		dobrze ? co dalej ?
3		4		3

30 maj 13:15

razor: Uzależnij długość wysokości od długości krawędzi

30 maj 13:16

Katti:

1		a² √3
	a * h =
2		4

	a √3
h =
	2

30 maj 13:18

Katti: a tą dużą wysokość to z tw. Pitagorasa ?

30 maj 13:19

razor: Chodzi mi o wysokość czworościanu, tak, z Pitagorasa

30 maj 13:21

Katti: straszne głupoty mi z tego wychodzą, ale ok. dzieki za chęci

30 maj 13:22

razor: To pokaż jak liczysz

30 maj 13:24

Katti:

	2
(		h)² + H² = a²
	3

4	a² √3
		+ H² = a²
9	4

	a² √3
H² = a² −
	9

pewnie źle z rysunku wzięłam

30 maj 13:28

razor:

	a√3		3a²
(		)² =
	2		4

30 maj 13:34

Katti: haha no przecież emotka

30 maj 13:35

Katti: a = 4 ? emotka

30 maj 13:37

razor: tak, ale nie to masz obliczyć

30 maj 13:39

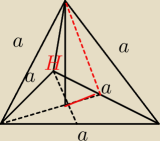
jerey: rysunek

	a√3
h=
	2

	a²√3
Pp=
	2

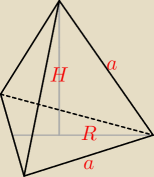
1		a√3
	h⇒
3		6

	a√3
(		)²+H²=h²
	6

	a√3		a√3
(		)²+H²=(		)²
	6		2

	3a²		3a²
H²=		−
	4		36

	27a²		3a²
H²=		−
	36		36

	24a²
H²=
	36

	2√6a
H=
	6

	1		a²√3
V=		*		*H
	3		4

16√2		a²√3
	=		*H
3		4

	64√2
H=
	a²√3

2√6		64√2
	=
6		a²√3

mnoże na krzyż 6√2a²=384√2 a²=64 a=8

	8√3
podstawiam do h=		⇒4√3
	2

30 maj 13:40

Katti: wiem, że mam obliczyć h, ale jak już mam a to już z górki. Poradziłam sobie, dzięki razor emotka

30 maj 13:41

razor: jerey, zgubiłeś a pod koniec emotka

30 maj 13:42

jerey:

	a√3
racja razor będzie a³=64 stąd a=4 i wstawiamy do h=		⇒2√3
	2

30 maj 13:45

jerey: przepraszam za błędy Katti zarówno w tym zadaniu jak i w poprzednim

30 maj 13:46

Bogdan: rysunek

Co za dużo (w tym przypadku obliczeń) to niezdrowo.

	1
Objętość czworościanu foremnego V =		a³√2 (nie ma potrzeby wyprowadzać
	12

tego wzoru).

1		16		12
	a³√2 =		√2 /*		⇒ a³ = 64 ⇒ a = 4
12		3		√2

	1
h =		*4√3 = 2√3
	2

30 maj 14:13

razor: Najpierw trzeba znać ten wzór Bogdan emotka

A jak się nie zna to trzeba liczyć

30 maj 14:17

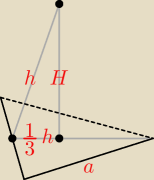
Bogdan: rysunek

	2
Z obliczeniami można tak: H = √h² − h²/9 =		h√2
	3

	1		1		h
h =		a√3 ⇒		a =
	2		2		√3

Objętość czworościanu

1		h		2		16
	*		h		h√2 =		√2 ⇒ h³ = 24√3 = (2√3)³ ⇒ h = 2√3
3		√3		3		3

30 maj 15:00