Trygonometria
Qmi:
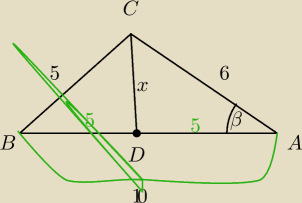
Oblicz długość środkowej |CD| w trójkącie ABC, jeśli dane są długości boków.
|AB|=10
|AC|=6
|CB|=5
Od czego zacząć?
Jeśli podstawiam do twierdzenia cosinusów to mam dwie nie wiadome.
30 maj 12:09
Qmi: Przepraszam za te zielone kreski, ale nie było ich widać jak rysowałem, teraz się pojawiły.
30 maj 12:10
30 maj 12:16
Qmi: Jednak chyba dałem radę z tym zadaniem.
| | 5 | | 1 | | 1 | |
Bo cos β = |
| z definicji = |
| = cos 60o = |
| |
| | 10 | | 2 | | 2 | |
Czyli później mamy.
x
2 = 5
2+6
2−2*5*6*cosβ
x
2=25+36−60cosβ
x
2=61−60cosβ
x
2=61−30
x
2=31
x=
√31
Git?
30 maj 12:19
kyrtap: | | 1 | |
Oblicz pole trójkąta ABC ze wzoru Herona, następnie korzystając ze wzoru P = |
| IADI IACI |
| | 2 | |
sinβobliczysz sinβ tylko jest teraz pytanie czy kąt alfa jest kątem ostrym

30 maj 12:22
Qmi: Z tego gotowego wzoru wyszło mi inaczej niż tutaj

Wyszło mi
30 maj 12:22
kyrtap: Qmi dobrze zrobiłeś

30 maj 12:23
kyrtap: Tylko jest pytanie czy β jest kątem ostrym ?
30 maj 12:24
Qmi: Kąt alfa nie jest podany. w szkole zastosowaliśmy tutaj tylko twierdzenie cosinusów i wyszło
(chyba dobrze), a robię je po raz drugi bo nie mam w całości tego zadania i nie wiem co z
czego wynika.
30 maj 12:24
jerey: albo tak?
w trójkącie BAC; β?
z tw cosinusów licze β
25=100+36−2*10*6cosβ
| | 111 | |
x2=62+52−2*5*6cos |
| |
| | 120 | |
dobra chyba moje jest źle xD
30 maj 12:25
kyrtap: Wiem wiem że nie jest podany ale mogli zaznaczyć że kąt β jest ostry
30 maj 12:25
bezendu:
jerey dobrze masz, trzeba umieć korzystać ze wzoru Qmi
c−długość boku na którą pada środkowa
| | 1 | | √22 | |
d= |
| *√2*52+2*62−102= |
| |
| | 2 | | 2 | |
30 maj 12:27
kyrtap: nie raczej dobrze masz jerey bo my nie wiemy czy ten β jest ostry
30 maj 12:27
Qmi: Które zrobiłem dobrze?
A do czego jest potrzebne to czy jest ostrym czy nie?
do tego czy jest ujemna wartość?
Zawsze można narysować bo mamy podane wartości

30 maj 12:27
kyrtap: Dla mnie to dużo daje bo wtedy wiem czy mogę zastosować jedynkę trygonometryczną czy nie
30 maj 12:28
jerey: ok
30 maj 12:28
kyrtap: jerey masz dobrze w takim razie

30 maj 12:28
kyrtap: bezendu też dobrze zrobił

30 maj 12:28
Qmi: bezendu, Twoim wzorem zrobiłem dobrze. Tyle samo Nam wyszło. tylko dlaczego wyszło mi inaczej
wyżej?
30 maj 12:29
jerey: 
30 maj 12:30
kyrtap: Bo ty uwzględniłeś że kąt β jest ostry gdzie w poleceniu nie ma o tym mowy
30 maj 12:30
jerey: | | 1 | |
Qmi na jakiej podstawie wywnioskowałes, ze cosB= |
| ? |
| | 2 | |
30 maj 12:31
jerey: cosβ*
30 maj 12:31
Qmi: Mój błąd, bo tam nie ma kąta prostego, w wziąłem to z definicji, ale tak jak mówię nie ma kąta
ostrego.
30 maj 12:32
Qmi: Zacząłem liczyć sposobem jerey i chyba zabłądziłem.
| | 111 | |
Cos β = |
| , to potrafiłem obliczyć, ale dalej. |
| | 120 | |
x
2=36+25−2*5*6*cosβ
30 maj 12:41
jerey: jest ok
Qmi x
2=61−(skróćmy to wyrażenie)55,5
x
2=61−55,5
x
2=5,5
| | 11 | | √11 | |
x2= |
| ⇒ x= |
| usuń niewymiernosć jest ok |
| | 2 | | √2 | |
30 maj 12:43
Qmi: Też dochodziłem do 5,5 ale nie potrafiłem tego tak rozbić. Dziękuje wszystkim za pomoc

30 maj 12:46
 Oblicz długość środkowej |CD| w trójkącie ABC, jeśli dane są długości boków.
|AB|=10
|AC|=6
|CB|=5
Od czego zacząć?
Jeśli podstawiam do twierdzenia cosinusów to mam dwie nie wiadome.
Oblicz długość środkowej |CD| w trójkącie ABC, jeśli dane są długości boków.
|AB|=10
|AC|=6
|CB|=5
Od czego zacząć?
Jeśli podstawiam do twierdzenia cosinusów to mam dwie nie wiadome.

 Wyszło mi
Wyszło mi






