Spr Paweł: Mam takie oto zadanie do sprawdzenia: ^−2x+1_2x−3 ≤ 5 wyliczam dziedzine: 2x − 3 ≠ 0 2x ≠ 3 / :2 x ≠ 3/2 ^−2x+1_2x−3 ≤ 5 ^−2x+1_2x−3 − 5 ≤ 0 ^−2x+1_2x−3 − ^5(2x−3)_2x−3 ≤ 0 ^{−2x+1−10x+15}_2x−3 ≤ 0 ^−12x+16_2x−3 ≤ 0 / * (2x−3)^{2 −12x+16}_2x−3 * (2x−3)² ≤ 0 (−12x + 16)(2x−3) ≤ 0 −12(x + ¹⁶₁₂) * 2(x− ³₂) ≤ 0 −24 (x + ¹⁶₁₂)(x− ³₂) ≤ 0 / : −24 (x + ¹⁶₁₂)(x− ³₂) ≤ 0 x1= −¹⁶₁₂ x2=³₂ 6/12 x∊<−¹⁶₁₂ ; ³₂ )

5-latek: po piersze przedzial powinien byc obustronnie domkniety bo masz ≤0 Ale tez jest zle wyznaczony bo jak mnozysz lub dzielisz nierownosc przez liczbe ujemna to zmieniasz jej zwrot na przeciwny (podzieliles przez −24

5-latek:

	3
A nie jednak nie powinien byc domkniety prawostronnie bo		nie nalezxy do dziedziny .
	2

Ale wyznaczony jest zle

Eta:

	3
x≠
	2

−2x+1−10x+15		16−12x
	≤0 ⇔		≤0 /:4
2x−3		2x−3

teraz równoważna postać iloczynowa (4−3x)(2x−3)≤0 miejsca zerowe

	4		3		3
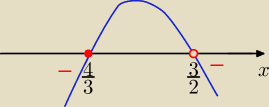
x=		v x=		i parabola ramionami do dołu i x≠
	3		2		2

	4		3
z wykresu: odp: x∊(−∞,		> U (		, ∞)
	3		2

5-latek: Witam i pozdrawiam

Paweł: dzieki, pozdrawiam cała ekipę