pomocy Kaśka_: Wyznacz wartość parametru m, m∊R, dla których równanie: a) sin x = m²−3 ma trzy rozwiązania w przedziale <0,2π> b) lcos xl = m²−4(m+1) ma trzy rozwiązania w przedziale <−π,π> c) sin x = m −2m ma cztery rozwiązania w przedziale (−π,2π)

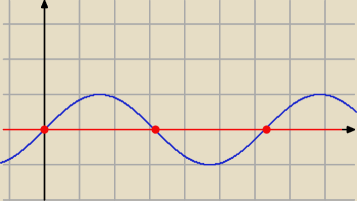
Godzio: a) m² − 3 = 0 ⇒ m = √3 lub m = − √3

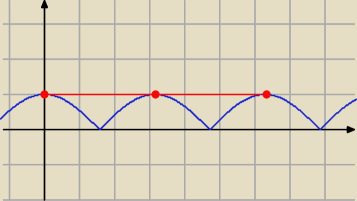
Godzio: b) m² − 4(m + 1) = 1 ⇒ m² − 4m − 5 = 0 ⇒ (m − 5)(m + 1) = 0 ⇒ m = 5 lub m = −1

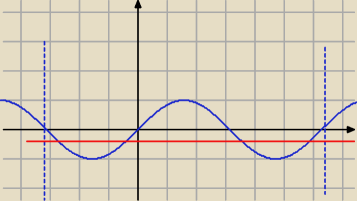
Godzio: b) wziąłem odruchowo przedział <0,2π>, ale identyczna prosta jest dla przedziału <−π,π> c) −1 < m² − 2m < 0 m² − 2m + 1 > 0 i m(m − 2) < 0 (m − 1)² > 0 i m(m − 2) < 0 m ≠ 1 i m ∊ (0,2) Odp: m ∊ (0,1) U (1,2)

ZKS: Godzio widziałeś BF3 jest za darmo.

Godzio: Widziałem, ale co mi po tym skoro mam go

Kaśka_: a taki d) ltgx − 1l =m²−6m ma dwa rozwiązania w przedziale <0,π>

Kaśka_: z tg jakoś nie rozumiem :x

Godzio: Narysuj sobie ten wykres to zrozumiesz

Kaśka_: tgx→u=[1,0] tg x−1 → ltg x−1l dobrze?

Kaśka_: oj przesunięcie powinno być o u=[0,−1]

Godzio: Tak, a później odbijasz to co jest na dole, na górę.

Kaśka_: dałam radę dzięki za wytłumaczenie